Si dimostri che l’equazione ![]() per
per ![]() ha un’unica radice reale e se ne calcoli un valore approssimato con due cifre decimali esatte.
ha un’unica radice reale e se ne calcoli un valore approssimato con due cifre decimali esatte.
Sia ![]()
Esistenza e unicità
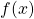 è continua in R
è continua in R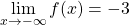
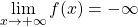
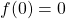
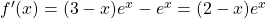
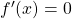
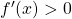 per
per 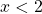 ,
, 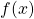 crescente
crescente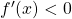 per
per 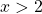 ,
, 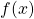 decrescente
decrescente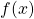 ha un massimo relativo per
ha un massimo relativo per 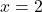
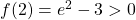
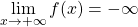 , per
, per 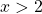 deve cambiare segno…
deve cambiare segno…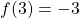
- Nell’intervallo
![Rendered by QuickLaTeX.com [2, 3]](https://www.valcon.it/math/wp-content/ql-cache/quicklatex.com-4d3acbceab9ef0f6340effc572ec16c4_l3.png) la funzione è continua, cambia di segno: esiste
la funzione è continua, cambia di segno: esiste 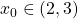 tale che
tale che 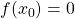
- Nell’intervallo
![Rendered by QuickLaTeX.com [2, 3]](https://www.valcon.it/math/wp-content/ql-cache/quicklatex.com-4d3acbceab9ef0f6340effc572ec16c4_l3.png) la funzione è decrescente, lo zero è unico.
la funzione è decrescente, lo zero è unico.
L’equazione ![]() per
per ![]() ha un’unica radice reale nell’intervallo
ha un’unica radice reale nell’intervallo ![]()
Approssimazione?
…