L’ennesima tecnica per realizzare immagini molto interessanti!
In alcuni casi si ottengono approssimazioni sempre più fedeli di frattali famosi.
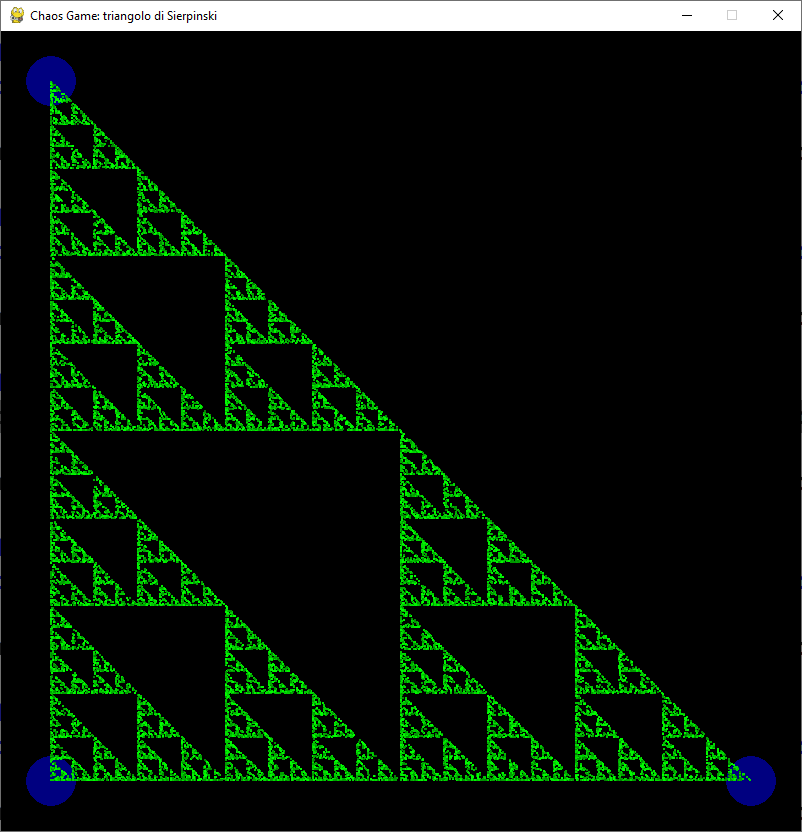
Triangolo di Sierpinski
Osserva la figura
- Fissa alcuni punti (blu) A, B, C su una superficie
- Scegli tra A, B, C il punto P1 dal quale partire (per esempio quello in alto a sinistra)
Colora il 1° punto verde P1 - Scegli tra A, B, C il punto X1 verso cui avanzare (per esempio quello in basso a sinistra)
Il punto medio tra P1 e X1 è il 2° punto verde P2 - Scegli tra A, B, C il punto X2 verso cui avanzare (per esempio quello in basso a sinistra)
Il punto medio tra P2 e X2 è il 3° punto verde P3 - …
- Scegli tra A, B, C il punto X5 verso cui avanzare (per esempio quello in basso a destra)
Il punto medio tra P5 e X5 è il 6° punto verde P6 - Scegli tra A, B, C il punto X6 verso cui avanzare (per esempio quello in basso a sinistra)
Il punto medio tra P6 e X6 è il 7° punto verde P7
Dopo un certo numero di passi ottieni un’approssimazione del triangolo di Sierpinski!
Variazioni…
Il risultato finale dipende da alcune scelte
- Il numero di punti fissi: 3, 4, 5, 6, …
- La disposizione dei punti fissi iniziali
- lungo i lati della superficie quadrata
- sui vertici di un poligono regolare
- anche uno al centro del quadrato/poligono?
- Il salto al prossimo punto avviene
- a metà della distanza
- a due terzi della distanza
- La scelta del prossimo punto è
- libera, un punto a caso tra tutti
- guidata, un punto a caso ma in un certo sottoinsieme dei punti (1°, 2°, 4° in senso orario…)
Prova!
- Python + Pygame
- Python + Turtle
- Small Basic
- …