Complessità: ricerche

Pagina 205 del testo

Ricerca sequenziale

Il codice analizzato è il seguente

def ricerca_sequenziale(vettore, n, x):
    trovato = False                      # c1
    i = 0                                # c2
    while(i < n) and (not trovato):      # c3 c4 c5
        if(vettore[i] == x):             # c6
            trovato = True               # c7
        i = i+1                          # c8
    return trovato                       # c9

Il codice presenta operazioni diverse (assegnazioni, confronti, aritmetiche, logiche).
Per semplificare i calcoli si decide di trascurare le differenze esistenti tra i tempi di esecuzione delle diverse operazioni e di stabilire un tempo costante per tutte.

I valori di T(n) sono

Vettore vuoto: c₁+c₂+(c₃+c₄+c₅)+c₉ = 6
Elemento in posizione 0: c₁+c₂+(c₃+c₄+c₅+c₆+c₇+c₈)+(c₃+c₄+c₅)+c₉ = 12
Elemento in posizione 1: c₁+c₂+(c₃+c₄+c₅+c₆+c₈)+(c₃+c₄+c₅+c₆+c₇+c₈)+(c₃+c₄+c₅)+c₉ = 17
Elemento in posizione 2: c₁+c₂+(c₃+c₄+c₅+c₆+c₈)+(c₃+c₄+c₅+c₆+c₈)+(c₃+c₄+c₅+c₆+c₇+c₈)+(c₃+c₄+c₅)+c₁₀ = 22
…
Elemento in posizione p: c₁+c₂+(c₃+c₄+c₅+c₆+c₈)+…+(c₃+c₄+c₅+c₆+c₈)+(c₃+c₄+c₅+c₆+c₇+c₈)+(c₃+c₄+c₅)+c₉ = 5*p+12
…
Elemento in posizione n-1: 5*(n-1)+12
Elemento non presente: 5*n+12

Analizziamo i casi più interessanti

Caso ottimo, quando il vettore è vuoto: T(n) = 6
… oppure l’elemento x compare alla posizione 0: T(n) = 12
Caso pessimo, l’elemento x compare alla posizione n-1: T(n) = 5*(n-1)+12
… oppure se l’elemento x non è presente: T(n) = 5n+12
Caso medio, supponiamo di effettuare n ricerche con l’elemento presente alle diverse posizioni 0, 1, …, n-1

T(n) = $\displaystyle \frac{12 + (5+12) + (5\cdot 2+12) + ... + [5\cdot (n-1)+12]}{n}$

= $\displaystyle 5\cdot \frac{1}{n}\cdot \sum_{i=0}^{n-1} i + 12$ = $\displaystyle 5\cdot \frac{1}{n}\cdot \frac{(n-1)\cdot n}{2} + 12$ = $\displaystyle 5\cdot \frac{n-1}{2} + 12$ = $2.5\cdot n + 9.5$ .

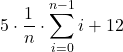Conclusioni

Il tempo richiesto dall’algoritmo di ricerca sequenziale è, tranne che nei casi banali, una funzione lineare di n, il numero di elementi presenti nel vettore: $T(n) = c_1 n + c_2$

Ricerca binaria

Analizziamo il codice

def ricerca_binaria(vettore, n, x):
    primo = 0                                  # c1
    ultimo = n-1                               # c2
    trovato = 0                                # c3
    while(primo <= ultimo) and (not trovato):  # c4 c5 c6
        centro = (primo+ultimo) // 2           # c7 
        if(vettore[centro] == x):              # c8
            trovato = centro                   # c9
        elif(vettore[centro] < x):             # c10
            primo = centro+1                   # c11
        else:
            ultimo = centro-1                  # c12
    return trovato                             # c13

Utilizzando la tecnica di calcolo della complessità in tempo utilizzata per la ricerca sequenziale, i valori di T(n) sono

Vettore vuoto: c₁+c₂+c₃+(c₄+c₅+c₆)+c₁₃ = 7
Elemento in 1° posizione centrale: c₁+c₂+c₃+(c₄+c₅+c₆+c₇+c₈+c₉)+(c₄+c₅+c₆)+c₁₃ = 13
Elemento in 2° posizione centrale: c₁+c₂+c₃+(c₄+c₅+c₆+c₇+c₈+c₁₀+c_11|12)+(c₄+c₅+c₆+c₇+c₈+c₉)+(c₄+c₅+c₆)+c₁₃ = 20
Elemento in 3° posizione centrale: c₁+c₂+c₃+(c₄+c₅+c₆+c₇+c₈+c₁₀+c_11|12)+(c₄+c₅+c₆+c₇+c₈+c₁₀+c_11|12)+(c₄+c₅+c₆+c₇+c₈+c₉)+(c₄+c₅+c₆)+c₁₃ = 27
…
Un accesso nel while senza successo richiede 7 operazioni, con successo 6.
Consideriamo un costo fisso 7…
Elemento trovato dopo m accessi: 7*m+13
Elemento non trovato dopo m accessi: 7*m+13

Analizziamo i casi più interessanti

Caso ottimo, quando il vettore è vuoto: T(n) = 7
… oppure l’elemento x compare alla posizione centrale: T(n) = 13
Caso pessimo, l’elemento x compare dopo m accessi: T(n) = 7*m+13
… oppure se l’elemento x non è presente: T(n) = 7*m+13

con m il numero di volte che viene eseguito il ciclo while.

Quanto vale m?

La dimensione del vettore sul quale si effettua la ricerca si dimezza a ogni passo

$n$ -> $\displaystyle \frac{n}{2}$ -> $\displaystyle \frac{n}{4}$ -> $\displaystyle \frac{n}{8}$ -> … -> 2 -> $\displaystyle \frac{n}{2^m}$ = 1

Quando il valore della potenza di 2 raggiunge n il ciclo termina sicuramente, cioè per

2^m= n
m = log₂n

quindi, nel caso pessimo: T(n) = 7log₂n + 13, quindi $T(n) = c_1 \log_2 n + c_2$

Confronto

Il numero di accessi è molto diverso

Ricerca sequenziale, mediamente: 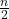$\frac{n}{2}$ , nel caso pessimo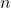 $n$
Ricerca binaria, nel caso pessimo: $\log_2 n$

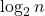
L’algoritmo di ricerca binaria ha un codice più lungo, utilizza più variabili locali, richiede un’addizione e una divisione… ipotizziamo che le costanti della sua complessità in tempo siano molto alte, per esempio 10, 20, … contrapposte a 5 e 10

Confrontiamo i valori delle due funzioni al variare di n

$T_{seq}(n) = 5 n + 10$
$T_{bin}(n) = 10 \log_2 n + 20$

n		T_seq(n)		T_bin(n)
4	= 2²	5·4+10	= 30	10·2+20	= 40
8	= 2³	5·8+10	= 50	10·3+20	= 50
16	= 2⁴	5·16+10	= 90	10·4+20	= 60
32	= 2⁵	5·32+10	= 170	10·5+20	= 70
64	= 2⁶	5·64+10	= 330	10·6+20	= 80
128	= 2⁷	5·128+10	= 650	10·7+20	= 90
256	= 2⁸	5·256+10	= 1.290	10·8+20	= 100
512	= 2⁹	5·512+10	= 2.570	10·9+20	= 110
1.024	= 2¹⁰	5·1.024+10	= 5.130	10·10+20	= 120
1.048.576	= 2²⁰	…	> 5*10^6	10·20+20	= 220
1.073.741.824	= 2³⁰	…	> 5*10^9	10·30+20	= 320

L’algoritmo di ricerca binaria (con strutture dati ordinate)

è più efficiente già con 16 elementi
e al crescere di n diventa irrinunciabile.