- Numero di combinazioni?
- Risolubilità?
- Numero di mosse minimo?
- …
Numero di combinazioni
Se si prende in considerazione un’ipotetica versione 2×2 e si fissa la casella vuota in basso a destra si possono comporre facilmente tutte le configurazioni
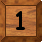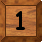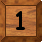   | | | 3 configurazioni possibili |
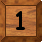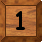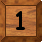| | | | 3 configurazioni impossibili |
Osserva: 3+3 = 6 = 3!.
Se la posizione della casella vuota è libera
4! = 4*3*2*1 = 24 = 12+12
Passando alla versione successiva 2×3 si possono comporre (?) 60 configurazioni possibili e 60 impossibili.
Osserva: 60+60 = 120 = 5!.
In generale, si può dimostrare che con n pezzi le combinazioni sono n! con 
combinazioni possibili e combinazioni impossibili