Indicatori – 1

di

Indici di tendenza centrale: Media aritmetica, Mediana, Moda

Media

Viene calcolata sommando tutti i valori a disposizione e dividendo il risultato per il numero complessivo dei dati.

\displaystyle M(X)= \displaystyle \frac{1}{n} \sum_{i=1}^n {x_i}= \displaystyle \sum_{i=1}^n {p_i\ x_i}
= \displaystyle \frac{x_1+x_2+\dots+x_n}{n}= p_1x_1+p_2x_2 + \dots + p_nx_n

Proprietà

  • \displaystyle M(X+b) = M(X)+b
  • \displaystyle M(aX) = a\ M(X)
  • \displaystyle M(aX+b) = a\ M(X)+b

Dimostrazioni

\displaystyle M(X+b)= \displaystyle \frac{1}{n} \sum_{i=1}^n {(x_i+b)}= \displaystyle \sum_{i=1}^n {p_i\ (x_i+b)}
= \displaystyle \frac{1}{n}\left( \sum_{i=1}^n x_i+ \sum_{i=1}^n b\right)= \displaystyle \sum_{i=1}^n {p_i \ x_i+\sum_{i=1}^n{p_i \ b}
= \displaystyle \frac{1}{n} \sum_{i=1}^n {x_i}+\frac{1}{n}\ n\ b= \displaystyle \sum_{i=1}^n {p_i \ x_i+b \sum_{i=1}^n{p_i}
= \displaystyle M(X)+b= \displaystyle M(X)+b
\displaystyle M(a X)= \displaystyle \frac{1}{n} \sum_{i=1}^n {a\ x_i}= \displaystyle \sum_{i=1}^n {p_i \ a \ x_i}
= \displaystyle a\ \frac{1}{n} \sum_{i=1}^n {x_i}= \displaystyle a\ \sum_{i=1}^n {p_i\ x_i}
= \displaystyle a\ M(X)= \displaystyle a\ M(X)

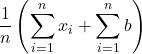Moda

Un valore della variabile casuale al quale corrisponde la massima frequenza

  • la moda non è definita se tutti i valori sono diversi
  • una distribuzione è unimodale se ammette un solo valore modale
  • una distribuzione è bimodale se esistono due valori che compaiono entrambi con la frequenza massima
    • Il risultato dipende dall’applicazione
      • Calc/Excel: il più piccolo
      • Fogli: il primo dei due nella lista
  • una distribuzione è trimodale se …
  • una distribuzione è multimodale se …

Mediana

Per calcolare la mediana di \displaystyle n dati

  • si ordinano gli 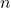\displaystyle n dati in ordine crescente
  • se il numero di dati è dispari la mediana corrisponde al valore centrale, ovvero al valore che occupa la posizione \displaystyle (n+1)/2
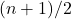
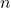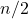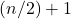  • se il numero \displaystyle n di dati è pari, la mediana è stimata utilizzando i due valori che occupano le posizioni \displaystyle n/2 e \displaystyle (n/2)+1 (generalmente si sceglie la loro media aritmetica se il carattere è quantitativo).

Classi

Se le modalità sono raggruppate in classi non si definisce un valore univoco, ma una classe mediana \displaystyle X_{i}-X_{i+1}.
La determinazione di tale classe avviene considerando le frequenze cumulate.

In alcuni casi si preferisce calcolare comunque un valore numerico approssimato interpolando i valori disponibili

\displaystyle X_i + \left(X_{i+1}-X_i\right) \frac{0,5-F_i}{F_{i+1}-F_i}, con F frequenze percentuali cumulate