Indicatori – 5

di

Covarianza

\displaystyle \sigma_{XY} = \frac{1}{n}\sum_{i=1}^{n} {(x_i-\overline{x})(y_i-\overline{y})}

Proprietà

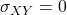  • \displaystyle \sigma_{XY}=0 ⇔ X e Y sono indipendenti
  • \displaystyle |\sigma_{XY}|\le \sigma_X \cdot \sigma_Y
  • \displaystyle \sigma_{XX}=var(X)
  • \displaystyle \sigma_{XY}=M(XY)-M(X)\cdot M(Y)

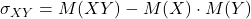
Dimostrazione

\displaystyle \sigma_{XY} = \frac{1}{n}\sum_{i=1}^{n}{(x_i-\overline{x})(y_i-\overline{y})}

\displaystyle =\frac{1}{n}\sum_{i=1}^{n}{\left(x_i \cdot y_i - x_i \cdot \overline{y} -\overline{x} \cdot y_i + {\overline{x}\cdot \overline{y}}\right)

\displaystyle =\frac{1}{n}\sum_{i=1}^{n}{x_i \cdot y_i} - \overline{y}\cdot \frac{1}{n}\sum_{i=1}^{n}{x_i} -\overline{x}\cdot \frac{1}{n}\sum_{i=1}^{n}{y_i} + \frac{1}{n}\sum_{i=1}^{n}{\overline{x}\cdot \overline{y}}

=M(XY)-M(X)\cdot M(Y)-M(X)\cdot M(Y)+M(X)\cdot M(Y)

=M(XY)-M(X)\cdot M(Y)

Indice di correlazione di Pearson
Indice di correlazione lineare
Coefficiente di correlazione

\displaystyle r=\frac{\sigma_{XY}}{\sigma_X \cdot \sigma_Y}

Proprietà

  • -1 <= r <= +1
  • 0 < r <= +1, correlazione positiva, diretta
  • -1 <= r < 0, correlazione negativa, inversa
  • r = -1, correlazione perfetta inversa
  • r = 0, non c’è correlazione lineare
  • r = +1, correlazione perfetta diretta