XXI Gara Nazionale a Squadre – Finale nazionale 17 settembre 2020 – Numero 3
Appena creato, il pupazzo di neve comincia a vaneggiare sparando problemi a raffica: per esempio, esclama
«Siano ![]() , per
, per ![]() , tutte le coppie ordinate di interi positivi che soddisfano
, tutte le coppie ordinate di interi positivi che soddisfano ![]() .»
.»
«Che carino! Lo chiamerò Olaforum, con tutti questi problemi», decide Gianna.
Ma il pupazzo la ignora e continua «Quanto vale il prodotto di tutti gli ![]() ?»
?»
Passo 1
- Le variabili
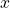 e
e 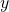 possono essere scambiate l’una con l’altra nella formula senza alterare il risultato.
possono essere scambiate l’una con l’altra nella formula senza alterare il risultato. - Se
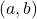 è una soluzione allora lo è anche
è una soluzione allora lo è anche  .
. - Cerchiamo le soluzioni
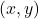 con
con 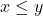 e dopo includiamo anche la soluzione
e dopo includiamo anche la soluzione 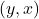
Passo 2
- Sia (x, x) una coppia soluzione

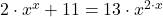
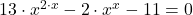
- …
- x = 1
- Infatti
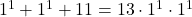
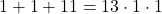
- 13 = 13
- L’unica soluzione con
 è
è 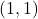 , tutte le eventuali altre saranno con
, tutte le eventuali altre saranno con 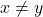
Passo 3
Proviamo le coppie (1,1), (1,2), (1,3), (1,4), (1,5)
| x=1 y=1 | x=1 y=2 | x=1 y=3 | x=1 y=4 | x=1 y=5 |
| 13 = 13 | 16 = 26 | 39 = 39 | 268 = 52 | 3137 = 65 |
Passo 4
Abbiamo individuato 3 soluzioni
- (1, 1)
- (1, 3)
- (3, 1)
Se non esistono altre soluzioni allora la risposta al quesito è
![]() =
= ![]() =
= ![]() = 200
= 200
Passo 5
- La risposta per ogni quesito deve essere compresa tra 0000 e 9999
- Se esiste un’altra soluzione
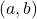 allora
allora 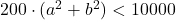
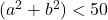
- Rimangono da controllare: (1, 6), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6), (4, 5)
- Completiamo la tabella precedente
| x=1 y=1 | x=1 y=2 | x=1 y=3 | x=1 y=4 | x=1 y=5 | x=1 y=6 |
| 13 = 13 | 16 = 26 | 39 = 39 | 268 = 52 | 3137 = 65 | 46668 = 78 |
| … | … | x=2 y=3 | x=2 y=4 | x=2 y=5 | x=2 y=6 |
| … | … | 42 = 936 | 271 = 3328 | 3140 = 10400 | 46671 = 29952 |
| … | … | … | x=3 y=4 | x=3 y=5 | x=3 y=6 |
| … | … | … | 276 = 67392 | 3163 = 394875 | 46694 = 2047032 |
| … | … | … | … | x=4 y=5 | … |
| … | … | … | … | 3392 = 8320000 | … |
Non esistono altre soluzioni…
Passo 6?
Esistono soluzioni con valori più grandi?
Osservazione 1
- Il secondo membro è un multiplo di 13 (è divisibile per 13)
- Il primo membro deve essere un multiplo di 13 (divisibile per 13)
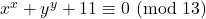
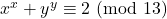
- Ci sono tre possibilità
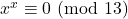 e
e 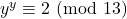
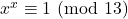 e
e 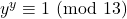
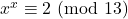 e
e 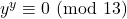
Osservazione 2
Calcoliamo il resto della divisione per 13 di ![]() al crescere della
al crescere della ![]()
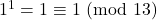
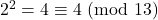
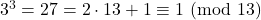
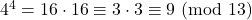
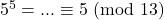
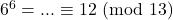
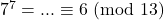
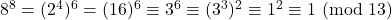
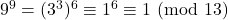
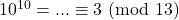
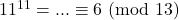
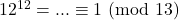
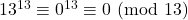
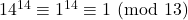
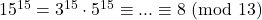
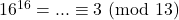
- …
Non compare il 2…