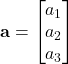 ,
, 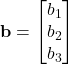
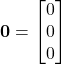
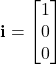 ,
, 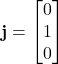 ,
, 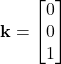
Prodotto per uno scalare
![]() =
= 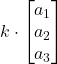 =
= 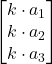
Proprietà
Somma
![]() =
= 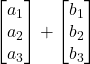 =
= 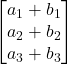
Proprietà
Opposto
![]() =
= ![]() =
= 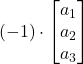 =
= ![]()
Proprietà
Sottrazione
![]() =
= 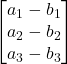
Proprietà
Prodotto scalare
![]() =
= 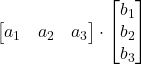 =
= ![]()
Proprietà
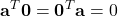
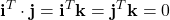
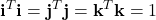
- …
Norma
Norma 1
![]()
= ![]()
La somma dei valori assoluti
Norma 2
![]()
Norma euclidea
Lunghezza
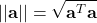
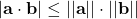
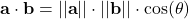
- …
Norma infinito
![]()
Norma infinito
Il valore assoluto maggiore