Considera la probabilità dei due eventi complementari al crescere di n (il numero di persone)
- p(“No”) = p(“nessuna coppia di compleanni coincidenti”)
- p(“Sì”) = p(“almeno una coppia di compleanni coincidenti”)
Considera il rapporto tra
- il numero di scelte per n giorni diversi ordinati
- il numero di scelte per n giorni ordinati
| n | p(“No”) | p(“Sì”) | |
|---|---|---|---|
| 0 | = 1 | = 0 | |
| 1 | = 1 | = 0 | |
| 2 | = 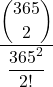 | = | = |
| 3 | = 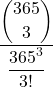 | = | = |
| 4 | = 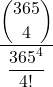 | = | = |
| … | … | … | |
= 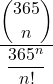 | = | = |