Complessità: asintotica

Dopo aver analizzato la complessità in tempo di alcuni algoritmi possiamo osservare che

il caso ottimo di un algoritmo è quasi sempre costante
non sarebbe significativo per la bassa probabilità che ha di presentarsi
il caso pessimo e il caso medio dipendono dalla dimensione dei dati
è difficile calcolare con precisione le costanti moltiplicative
per n piccolo è difficile decidere tra due algoritmi
per n abbastanza grande la differenza di comportamento diventa evidente

Per dare una misura della complessità in tempo di un algoritmo si preferisce

dare una misura approssimata del calcolo del tempo di esecuzione $T(n)$
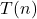
studiare il caso pessimo oppure il caso medio
valutare il comportamento per 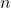$n$ sufficientemente grande… si introduce la complessità asintotica

Definizione

Una funzione $g(n)$ è $O(f(n))$ , e si legge $g(n)$ è dell’ordine o grande di $f(n)$ , se esistono una costante moltiplicativa $c$ ed un numero naturale $n_0$ tali che $g(n)\leq c\cdot f(n)$ per una certa $c$ e per ogni $n > n_0$

Esempio

Data la funzione $g(n)=2 n^2 + 4 n + 2$ , scegliendo opportunamente i valori ( $c=3$ , $n_0 > 5$ ) si ha

$g(5) = 72 < 75 = 3\cdot (5)^2$

allora $g(n)\leq c\cdot f(n)$ per $n \geq 5$ e quindi $g(n) \in O(n^2)$

In pratica

le costanti moltiplicative diventano trascurabili
le combinazioni lineari di funzioni diventano trascurabili
è sufficiente individuare la funzione più pesante
tutte le funzioni costanti sono dell’ordine $O(1)$
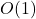
tutte le funzioni lineari sono dell’ordine $O(n)$
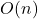
tutte le funzioni quadratiche sono dell’ordine $O(n^2)$
…

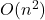
La complessità in tempo viene riassunta in una funzione più significativa che rappresenta la complessità in tempo asintotica.

Esempi

Le costanti moltiplicative sono volutamente sbilanciate per evidenziare l’aspetto asintotico… della complessità

$T_1(n) = 2\cdot n + 400\cdot \log_2 n \in O(n)$
$T_2(n) = 2\cdot n^3 + 400\cdot n \in O(n^3)$
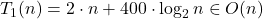
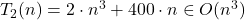
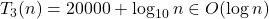$T_3(n) = 20000 + \log_{10}n \in O(\log n)$ , rifletti…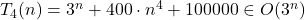
$T_4(n) = 3^n + 400\cdot n^4 + 100000 \in O(3^n)$

Elenco

Per tutte le semplificazioni che abbiamo adottato le funzioni di complessità veramente interessanti in ambito informatico sono poche

$O(1)$	Costante	Assegnazione…
$O(\log\log n)$	Sottologaritmica, meno di logaritmica
$O(\log n)$	Logaritmica	Ricerca binaria
$O(n^k)$ , 0 < k < 1	Sottolineare, meno di lineare, $\sqrt{n}$
$O(n)$	Lineare	Ricerca sequenziale
$O(n \log n)$	Enne-log-enne	Algoritmi di ordinamento evoluti
$O(n^k)$ , 1 < k < 2	Meno di quadratica	Algoritmi di ordinamento intermedi
$O(n^2)$	Quadratica	Algoritmi di ordinamento ingenui
$O(n^k)$ , 2 < k < 3	Meno di cubica
$O(n^3)$	Cubica	Prodotto di matrici scolastico
$O(n^k)$ , k ≥ 3	Polinomiale
$O(2^n)$	Esponenziale, con base 2	Torre di Hanoi
$O(k^n)$	Esponenziale, con base k > 1	Password
$O(n!)$	Fattoriale, più che esponenziale…	Anagrammi
$O(n^n)$	Più che esponenziale…