Complessità: fattoriale

Vedi esercizio numero 12 di pagina 202 del libro di testo

Versione iterativa

def f(n):
    prodotto=1                 # f1
    i=1                        # f2   
    while(i <= n):             # f3
        prodotto = prodotto*i  # f4
        i = i+1                # f5  
    return prodotto            # f6

n = int(input("n = "))         # m1 
x = f(n)                       # m2
print("Il fattoriale di", 
      n, "=", x)               # m3

T(n) = m1 + m2 + […] + m3
= m1+m2+[f1+f2+{…}+f6]+m3
= m1+m2+[f1+f2+{(f3+f4+f5)*n+f3}+f6]+m3
= (3n+4)+3
= 3*n+7

Versione ricorsiva

def f(n):
    if(n < 2):           # f1
        return 1         # f2
    else:          
        return n*f(n-1)  # f3 f4 f5

n = int(input("n = "))   # m1 
x = f(n)                 # m2
print("Il fattoriale di", 
      n, "=", x)         # m3

T(0) = m1 + m2 + (f1+f2) + m3 = 5
T(1) = m1 + m2 + (f1+f2) + m3 = 5
T(2) = m1 + m2 + (f1+f3+f4+f5)+(f1+f2) + m3 = 9
T(3) = m1 + m2 + (f1+f3+f4+f5)+(f1+f3+f4+f5)+(f1+f2) + m3 = 13
…

Cioè

Se n < 2: T(n) = 5
Se n 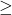$\ge$ 2: T(n) = 4*n+1

La ricorsione sostituisce l’iterazione e non cambia significativamente il tempo di esecuzione.

Versione con formula

$\displaystyle n! \approx \sqrt{2 \pi n}\left(\frac{n}{e}\right)^n$

In ordine di esecuzione (le operazioni sono molto diverse tra loro…)

T(n) = p1 + p2 + r1 + d1 + e1 + p3 = 6

Confronto

Consideriamo i pro e i contro di ognuno

Algoritmo	T(n)	O(f(n))	Pro	Contro
Iterativo	$c_{11}\cdot n + c_{12}$	$O(n)$	Codifica semplice	~n moltiplicazioni
Ricorsivo	$c_{21}\cdot n + c_{22}$	$O(n)$	Codifica corta, elegante	~n moltiplicazioni ~n chiamate ricorsive
Con formula	$c_{3}$	$O(1)$	Numero di operazioni costante	1. Difficile da ricordare 2. Numeri irrazionali 3. Valore approssimato

Conclusioni

Per il calcolo del fattoriale di n esistono più algoritmi
Le complessità in tempo …
Le complessità in tempo asintotiche …
Quale algoritmo scegliere al variare di n?
- Algoritmo ricorsivo, se n è piccolo
- Algoritmo iterativo, sempre conveniente
- Con formula, solamente se n è mooooolto grande e NON è necessario il valore esatto.