Pagina 207 del libro di testo
Dato un problema P si possono individuare diversi algoritmi risolutivi A1, A2, … ciascuno con la sua complessità in tempo T1, T2, …
Sia A* l’algoritmo con la complessità minima T*.
A* è un algoritmo ottimo per il problema P.
Se si dimostra che per il problema P non può esistere un algoritmo con complessità in tempo minore di T* allora il problema P ha complessità T*.
La complessità di un problema P è quella del suo algoritmo ottimo…
Per ogni problema
- la complessità in tempo e la complessità in spazio sono collegate tra loro
- esiste una complessità del problema sotto la quale non si può scendere
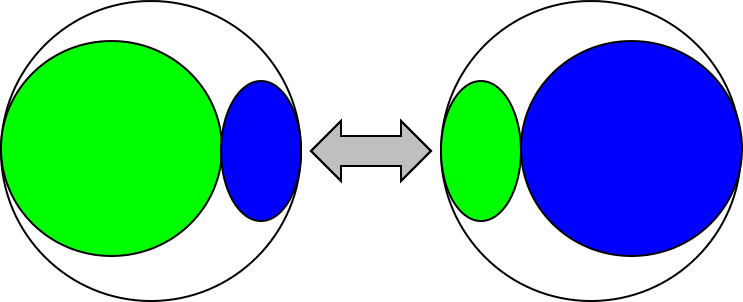
In pratica, per un certo problema posso scegliere un algoritmo/programma che utilizza
- codice molto lungo
- piccole quantità di dati
- codice molto corto
- grandi quantità di dati.
Se la complessità in tempo migliora a scapito della complessità in spazio forse non è conveniente…
Esempio
Calcolare il seno di un certo angolo
- Per ogni angolo il codice calcola il valore della funzione seno con un metodo di approssimazione.
- Codice lungo e lento.
- Poco spazio occupato in memoria.
- Una tabella contiene un certo numero di valori già calcolati della funzione seno, il codice consulta semplicemente la tabella.
- Codice corto e veloce.
- Tanto spazio occupato in memoria.
Analogamente per
- i numeri irrazionali, trascendenti…
- le note e gli strumenti della scheda audio…
- le geometrie della scheda video…