Complessità in tempo

di

Considera gli esempi del libro di testo a pagina 198 e successive.
La codifica in Python è più leggibile?

1

print("n = ")     # costo=1
n = int(input())  # costo=1
i = i+1           # costo=1

T(n) = 1+1+1 = 3

Per semplificare i calcoli associamo alle tre istruzioni un costo unitario ma in realtà hanno tempi d’esecuzione molto diversi

  1. istruzione di output, 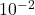10^{-2} s
  2. istruzione di input, 1 s
  3. addizione e assegnazione, 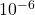10^{-6} s

2

print("n = ")        # c1
n = int(input())     # c2
i = 1                # c3
somma = 0            # c4
while(i <= n):       # c5
    somma = somma+i  # c6
    i = i+1          # c7
print("La somma dei primi", 
      n, "numeri è", somma)  # c8

T(n) = c1 + c2 + c3 + c4 + […] + c8
= c1+c2+c3+c4+[(c5+c6+c7)*n+c5]+c8
= [3*n+1]+5
= 3 n + 6

3.1

if(y > 0):  # c1
    r = 1   # c2
    z = 2   # c3
  1. Se l’if(..) ha successo
    T1(n) = c1 + c2 + c3 = 1+1+1 = 3
  2. Se l’if(...) fallisce
    T2(n) = c1 = 1
  3. Quindi: T(n) = 3

3.2

if(y > 0):  # c1
    r = 1   # c2
else:
    z = 2   # c3
    p = 0   # c4
    r = 2   # c5
  1. Se l’if(..) ha successo
    T1(n) = c1 + (c2) = 1+1 = 2
  2. Se l’if(...) fallisce
    T2(n) = c1 + (c3+c4+c5) = 1+1+1+1 = 4
  3. Quindi: T(n) = 4

4

def Somma(x, y):
    s = x+y                  # f1
    return s                 # f2
 
print("n = ")                # c1
n = int(input())             # c2
i = 1                        # c3
somma = 0                    # c4  
while(i <= n):               # c5
    somma = Somma(i, somma)  # c6 c7
    i = i+1                  # c8
print("La somma dei primi", 
      n, "numeri è", somma)  # c9

T(n) = c1+c2+c3+c4+[…]+c9
= (c5+c6+c7+[…]+c8)*n+c5 + 5
= (c5+c6+c7+f1+f2+c8)*n+c5 + 5
= 6 n + 6

5

if(x > 0):      # c1
    if(y > 0):  # c2
        r = 1   # c3
    else: 
        r = 2   # c4
        t = 1   # c5
    z = 3       # c6
  1. T1(n) = c1 = 1
  2. T2(n) = c1 + c2 + (c3) + c6 = 4
  3. T3(n) = c1 + c2 + (c4+c5) + c6 = 5
  4. T(n) = 5

6

i = 0          # c1
while(i < n):  # c2
    i = i+1    # c3

T(n) = c1 + […]
= c1 + [(c2+c3)*n + c2]
= 2 n + 2

7

Il costrutto repeat ... until ... non è presente in Python

8

L’istruzione for è tradotta in while per evidenziare le singole istruzioni

def SommaNumeriPari(n):
    m = 0           # c1
    i = 1           # c2
    while(i <= n):  # c3
        p = 2*i     # c4
        m = m+p     # c5
        i = i+1     # c6
    return m        # c7

T(n) = c1 + c2 + […] + c7
= c1+c2+[(c3+c4+c5+c6)*n+c3]+c7
= 4 n + 4

9

i = 0             # c1
while(i < 2*n):   # c2
    i = i+1       # c3
    j = j*3+4367  # c4

T(n) = c1 + (c2+c3+c4)*(2*n) + c2
= 6 n + 2

10

L’istruzione for è tradotta in while per evidenziare le singole istruzioni.
Attenzione al while interno…

i = 0                   # c1
while(i < n):           # c2
    j = 1               # c3
    while(j <= n):      # c4
        print("CIAO")   # c5
        j = j+1         # c6
    i = i+1             # c7
  1. Il while esterno cicla n volte
  2. Il while interno cicla n volte
  3. Il messaggio CIAO verrà visualizzato n^2 volte

T(n) = c1 + […]
= c1+(c2+c3+[…]+c7)*n+c2
= c1+(c2+c3+[(c4+c5+c6)*n+c4]+c7)*n+c2
= ([3*n+3]+1)*n+2
= (3*n+4)*n+2
= 3n^2+4 n+2

11

Le istruzioni for sono tradotte in while per evidenziare le singole istruzioni

def Funzione(n, m):
    x = 0               # c1
    i = 1               # c2
    while(i <= n):      # c3
        j = 1           # c4
        while(j <= m):  # c5
            x = x+1     # c6
            y = x       # c7
            j = j+1     # c8
        i = i+1         # c9
    return x            # c10
  1. Il while esterno cicla n volte
  2. Il while interno cicla m volte

T(n) = c1+c2+(c3+c4+[…]+c9)*n+c3+c10
= c1+c2+(c3+c4+[(c5+c6+c7+c8)*m+c5]+c9)*n+c3+c10
= (4*m+4)*n+4
= 4 m\cdot n + 4 n + 4