La congettura (probabilmente vera ma non ancora dimostrata) afferma che se si applica ripetutamente la formula
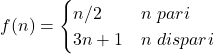
si giunge sempre al valore 1, indipendentemente dal valore di partenza (Wikipedia: Congettura di Collatz)
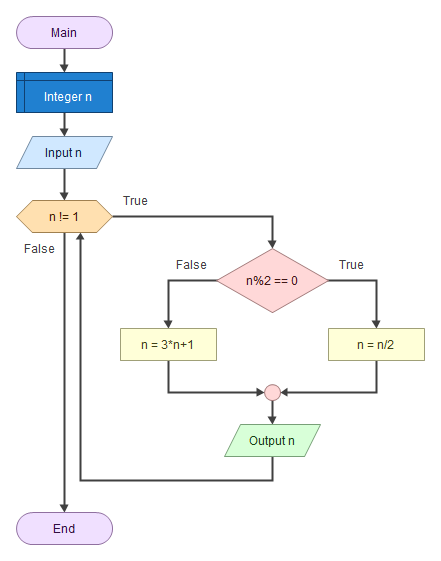
In tutti i casi quando si arriva al valore 1 si interrompe l’esecuzione, altrimenti la sequenza continuerebbe per sempre come
4 –> 2 –> 1 -> 4 –> 2 –> 1 …
Esempio
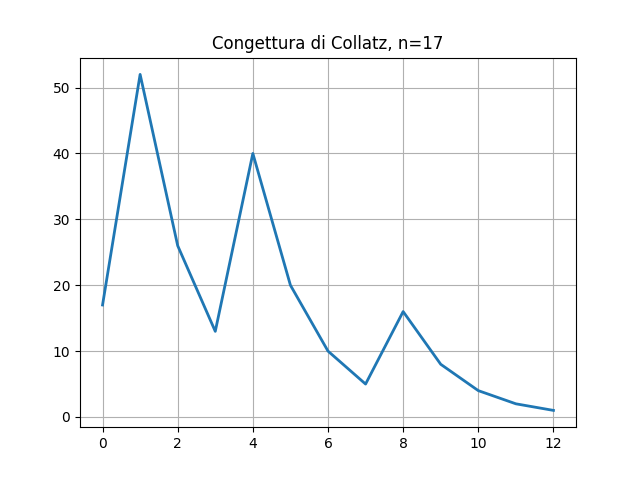
Ecco la sequenza che comincia da 17
| n | ? | |
|---|---|---|
| 17 | Dispari | 3*17 +1 |
| 52 | Pari | 52/2 |
| 26 | Pari | 26/2 |
| 13 | Dispari | 3*13 +1 |
| 40 | Pari | 40/2 |
| 20 | Pari | 20/2 |
| 10 | Pari | 10/2 |
| 5 | Dispari | 3*5 +1 |
| 16 | Pari | 16/2 |
| 8 | Pari | 8/2 |
| 4 | Pari | 4/2 |
| 2 | Pari | 2/2 |
| 1 | STOP |
Alcuni numeri percorrono una distanza molto grande prima di giungere a 1, altri raggiungono valori molto alti prima di precipitare verso 1.
La sequenza
17 -> 52 -> 26 -> 13 -> 40 -> 20 -> 10 -> 5 -> 16 -> 8 -> 4 -> 2 -> 1
ha distanza=12 e altezza=52
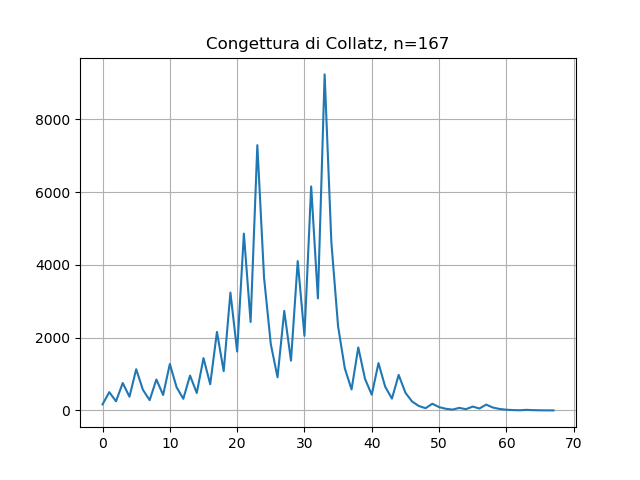
La sequenza 167 -> … -> 1 ha distanza=67 e altezza=9232!