Analisi di TRE dadi

di

Conteggi…

EsitoNumero
comb.		Prob.
31+1+1     1\displaystyle \frac{1}{216} = 0,4… %
41+1+2
1+2+1		2+1+1    3\displaystyle \frac{3}{216}= \displaystyle \frac{1}{72}= 1,3… %
51+1+3
1+2+2
1+3+1		2+1+2
2+2+1		3+1+1   6\displaystyle \frac{6}{216}= \displaystyle \frac{1}{36}= 2,7… %
61+1+4
1+2+3
1+3+2
1+4+1		2+1+3
2+2+2
2+3+1		3+1+2
3+2+1		4+1+1  10\displaystyle \frac{10}{216}= \displaystyle \frac{5}{108}= 4,6… %
71+1+5
1+2+4
1+3+3
1+4+2
1+5+1		2+1+4
2+2+3
2+3+2
2+4+1		3+1+3
3+2+2
3+3+1		4+1+2
4+2+1		5+1+1 15\displaystyle \frac{15}{216}= \displaystyle \frac{5}{72}= 6,9… %
81+1+6
1+2+5
1+3+4
1+4+3
1+5+2
1+6+1		2+1+5
2+2+4
2+3+3
2+4+2
2+5+1		3+1+4
3+2+3
3+3+2
3+4+1		4+1+3
4+2+2
4+3+1		5+1+2
5+2+1		6+1+121\displaystyle \frac{21}{216}= \displaystyle \frac{7}{72}= 9,7… %
91+2+6
1+3+5
1+4+4
1+5+3
1+6+2		2+1+6
2+2+5
2+3+4
2+4+3
2+5+2
2+6+1		3+1+5
3+2+4
3+3+3
3+4+2
3+5+1		4+1+4
4+2+3
4+3+2
4+4+1		5+1+3
5+2+2
5+3+1		6+1+2
6+2+1		25\displaystyle \frac{25}{216}= \displaystyle \frac{25}{216}= 11,5… %
101+3+6
1+4+5
1+5+4
1+6+3		2+2+6
2+3+5
2+4+4
2+5+3
2+6+2		3+1+6
3+2+5
3+3+4
3+4+2
3+5+2
3+6+1		4+1+5
4+2+4
4+3+3
4+4+2
4+5+1		5+1+4
5+2+3
5+3+2
5+4+1		6+1+3
6+2+2
6+3+1		27\displaystyle \frac{27}{216}= \displaystyle \frac{1}{8}= 12,5 %
111+4+6
1+5+5
1+6+4		2+3+6
2+4+5
2+5+4
2+6+3		3+2+6
3+3+5
3+4+4
3+5+3
3+6+2		4+1+6
4+2+5
4+3+4
4+4+3
4+5+2
4+6+1		5+1+5
5+2+4
5+3+3
5+4+2
5+5+1		6+1+4
6+2+3
6+3+2
6+4+1		27\displaystyle \frac{27}{216}= \displaystyle \frac{1}{8}= 12,5 %
121+5+6
1+6+5		2+4+6
2+5+5
2+6+4		3+3+6
3+4+5
3+5+4
3+6+3		4+2+6
4+3+5
4+4+4
4+5+3
4+6+2		5+1+6
5+2+5
5+3+4
5+4+3
5+5+2
5+6+1		6+1+5
6+2+4
6+3+3
6+4+2
6+5+1		25\displaystyle \frac{25}{216}= \displaystyle \frac{25}{216}= 11,5… %
131+6+62+5+6
2+6+5		3+4+6
3+5+5
3+6+4		4+3+6
4+4+5
4+5+4
4+6+2		5+2+6
5+3+5
5+4+4
5+5+3
5+6+2		6+1+6
6+2+5
6+3+4
6+4+3
6+5+2
6+6+1		21\displaystyle \frac{21}{216}= \displaystyle \frac{7}{72}= 9,7… %
14 2+6+63+5+6
3+6+5		4+4+6
4+5+5
4+6+4.		5+3+6
5+4+5
5+5+4
5+6+3		6+2+6
6+3+5
6+4+4
6+5+3
6+6+2		15\displaystyle \frac{15}{216}= \displaystyle \frac{5}{72}= 6,9… %
15  3+6+64+5+6
4+6+5		5+4+6
5+5+5
5+6+4		6+3+6
6+4+5
6+5+4
6+6+3		10\displaystyle \frac{10}{216}= \displaystyle \frac{5}{108}= 4,6… %
16   4+6+65+5+6
5+6+5		6+4+6
6+5+5
6+6+4		6\displaystyle \frac{6}{216}= \displaystyle \frac{1}{36}= 2,7… %
17    5+6+66+5+6
6+6+5		3\displaystyle \frac{3}{216}= \displaystyle \frac{1}{72}= 1,3… %
18     6+6+61\displaystyle \frac{1}{216} = 0,4… %
2161

Sia X la variabile casuale “somma dei punti realizzati lanciando tre dadi”, allora

\displaystyle x_i\displaystyle p_i\displaystyle p_i\cdot x_i\displaystyle x_i^2\displaystyle p_i\cdot x_i^2\displaystyle |x_i-m|\displaystyle p_i|x_i-m|\displaystyle (x_i-m)^2\displaystyle p_i(x_i-m)^2
3\displaystyle \frac{1}{216}\displaystyle \frac{1}{72}9\displaystyle \frac{1}{24}\displaystyle \frac{15}{2}\displaystyle \frac{5}{144}\displaystyle \frac{225}{4}\displaystyle \frac{25}{96}
4\displaystyle \frac{1}{72}\displaystyle \frac{1}{18}16\displaystyle \frac{2}{9}\displaystyle \frac{13}{2}\displaystyle \frac{13}{144}\displaystyle \frac{169}{4}\displaystyle \frac{169}{288}
5\displaystyle \frac{1}{36}\displaystyle \frac{5}{36}25\displaystyle \frac{25}{36}\displaystyle \frac{11}{2}\displaystyle \frac{11}{72}\displaystyle \frac{121}{4}\displaystyle \frac{121}{144}
6\displaystyle \frac{5}{108}\displaystyle \frac{5}{18}36\displaystyle \frac{5}{3}\displaystyle \frac{9}{2}\displaystyle \frac{5}{24}\displaystyle \frac{81}{4}\displaystyle \frac{15}{16}
7\displaystyle \frac{5}{72}\displaystyle \frac{35}{72}49\displaystyle \frac{245}{72}\displaystyle \frac{7}{2}\displaystyle \frac{35}{144}\displaystyle \frac{49}{4}\displaystyle \frac{245}{288}
8\displaystyle \frac{7}{72}\displaystyle \frac{7}{9}64\displaystyle \frac{56}{9}\displaystyle \frac{5}{2}\displaystyle \frac{35}{144}\displaystyle \frac{25}{4}\displaystyle \frac{175}{288}
9\displaystyle \frac{25}{216}\displaystyle \frac{25}{24}81\displaystyle \frac{75}{8}\displaystyle \frac{3}{2}\displaystyle \frac{25}{144}\displaystyle \frac{9}{4}\displaystyle \frac{25}{96}
10\displaystyle \frac{1}{8}\displaystyle \frac{5}{4}100\displaystyle \frac{25}{2}\displaystyle \frac{1}{2}\displaystyle \frac{1}{16}\displaystyle \frac{1}{4}\displaystyle \frac{1}{32}
11\displaystyle \frac{1}{8}\displaystyle \frac{11}{8}121\displaystyle \frac{121}{8}\displaystyle \frac{1}{2}\displaystyle \frac{1}{16}\displaystyle \frac{1}{4}\displaystyle \frac{1}{32}
12\displaystyle \frac{25}{216}\displaystyle \frac{25}{18}144\displaystyle \frac{50}{3}\displaystyle \frac{3}{2}\displaystyle \frac{25}{144}\displaystyle \frac{9}{4}\displaystyle \frac{25}{96}
13\displaystyle \frac{7}{72}\displaystyle \frac{91}{72}169\displaystyle \frac{1183}{72}\displaystyle \frac{5}{2}\displaystyle \frac{35}{144}\displaystyle \frac{25}{4}\displaystyle \frac{175}{288}
14\displaystyle \frac{5}{72}\displaystyle \frac{35}{36}196\displaystyle \frac{245}{18}\displaystyle \frac{7}{2}\displaystyle \frac{35}{144}\displaystyle \frac{49}{4}\displaystyle \frac{245}{288}
15\displaystyle \frac{5}{108}\displaystyle \frac{25}{36}225\displaystyle \frac{125}{12}\displaystyle \frac{9}{2}\displaystyle \frac{5}{24}\displaystyle \frac{81}{4}\displaystyle \frac{15}{16}
16\displaystyle \frac{1}{36}\displaystyle \frac{4}{9}256\displaystyle \frac{64}{9}\displaystyle \frac{11}{2}\displaystyle \frac{11}{72}\displaystyle \frac{121}{4}\displaystyle \frac{121}{144}
17\displaystyle \frac{1}{72}\displaystyle \frac{17}{72}289\displaystyle \frac{289}{72}\displaystyle \frac{13}{2}\displaystyle \frac{13}{144}\displaystyle \frac{169}{4}\displaystyle \frac{169}{288}
18\displaystyle \frac{1}{216}\displaystyle \frac{1}{12}324\displaystyle \frac{3}{2}\displaystyle \frac{15}{2}\displaystyle \frac{5}{144}\displaystyle \frac{225}{4}\displaystyle \frac{25}{96}
 1\displaystyle \frac{21}{2} 119 \displaystyle \frac{29}{12}340\displaystyle \frac{35}{4}
  \displaystyle M(X) \displaystyle M(X^2) \displaystyle \delta(X)\displaystyle dev(X)\displaystyle var(X)

Osserva

Media\displaystyle M(X)= \displaystyle \sum_i p_i\cdot x_i= \displaystyle \frac{21}{2}
Scarto medio assoluto\displaystyle \delta(X)= \displaystyle \sum _{i}p_i|x_{i}-m|}= \displaystyle \frac{29}{12}
Devianza\displaystyle dev(x)= \displaystyle \sum_{i}(x_i-m)^2= 340
Varianza\displaystyle var(X)= \displaystyle \sum_i p_i(x_i-m)^2= \displaystyle \frac{35}{4}
Deviazione standard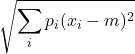\sigma (X)= \displaystyle \sqrt{\sum_i p_i(x_i-m)^2}= \displaystyle \frac{\sqrt{35}}{2}}
Deviazione standard relativa\displaystyle \sigma^{*}(X)= \displaystyle \frac{\sigma(X)}{|M(X)|}= \displaystyle \frac{\sqrt{35}}{21}}
…\displaystyle M(X^2)= \displaystyle \sum_ip_i\cdot x_i^2= 119
Varianzavar(X)= \displaystyle M(X^2)-[M(X)]^2= \displaystyle 119-\left(\frac{21}{2}\right)^2 = \displaystyle \frac{35}{4}