Le proposizioni sono affermazioni che possono essere o vere o false.
La logica proposizionale è costituita da:
- simboli di proposizione: p, q, r, s, …, X, Y, …
- connettivi logici
- Logica: Negazione, Congiunzione (et), Disgiunzione (vel), Implicazione, Coimplicazione
- Simboli: ¬, ∧, ∨, ⇒, ⇔
- Linguaggi di programmazione: NOT, AND, OR, XOR
- Foglio di calcolo: NON(), E(), O(), XOR()
- parentesi: (, )
- valore FALSO (F, False, F, 0)
- valore VERO (V, True, T, 1)
NOT, NON(), ¬, Negazione, non
p NOT p
+-------+-------+
| FALSO | VERO |
| VERO | FALSO |
+-------+-------+
Osserva
- VERO se p è FALSO
- FALSO se p è VERO
OR, O(), ∨, Disgiunzione, o, vel
p q p OR q
+-------+-------+--------+
| FALSO | FALSO | FALSO |
| FALSO | VERO | VERO |
| VERO | FALSO | VERO |
| VERO | VERO | VERO |
+-------+-------+--------+
Osserva
- VERO se almeno uno tra p e q è VERO
- FALSO se entrambi p e q sono FALSO
AND, E(), ∧, Congiunzione, e, et
p q p AND q
+-------+-------+---------+
| FALSO | FALSO | FALSO |
| FALSO | VERO | FALSO |
| VERO | FALSO | FALSO |
| VERO | VERO | VERO |
+-------+-------+---------+
Osserva
- VERO se entrambi p e q sono VERO
- FALSO se almeno uno tra p e q è FALSO
Proprietà
Per semplificare si utilizzano le abbreviazioni 0 / 1 per i valori logici Falso / Vero
a ¬a
+---+----+
| 0 | 1 |
| 1 | 0 |
+---+----+
a b a∨b a∧b
+-----+-----+-----+
| 0 0 | 0 | 0 |
| 0 1 | 1 | 0 |
| 1 0 | 1 | 0 |
| 1 1 | 1 | 1 |
+-----+-----+-----+
Verifica le seguenti uguaglianze confrontando le tabelle di verità corrispondenti
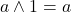
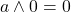
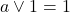
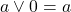
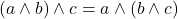 , associatività and
, associatività and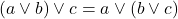 , associatività or
, associatività or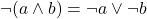 , Legge di De Morgan
, Legge di De Morgan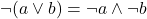 , Legge di De Morgan
, Legge di De Morgan- …