Soluzione 1
Risolvere un’equazione di primo grado ax+b=0, dati i valori dei coefficienti a e b
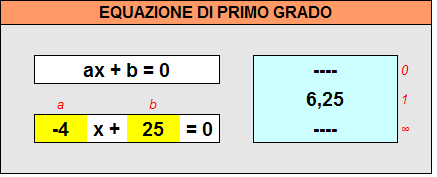
- (x) = -b/a
Se a=0 si ottiene un messaggio d’errore #DIV/0! .
Soluzione 2
Modifica la formula in modo che tenga conto del caso a=0.
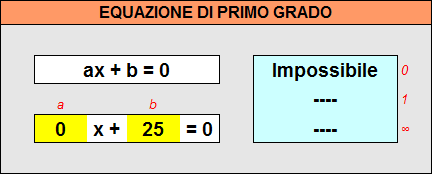
- (x) = SE(a <> 0; -b/a; "Impossibile")
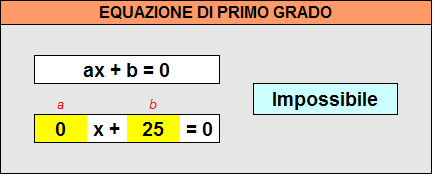
Nel caso in cui fosse anche b=0 allora l’equazione sarebbe indeterminata.
Soluzione 3
Modifica ancora la formula annidando una funzione SE() dentro l’altra
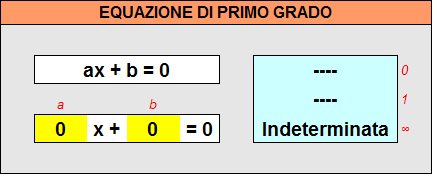
- (x) = SE(a <> 0; -b/a; SE(b <> 0; "Impossibile"; "Indeterminata"))
oppure
- (x) = SE(a <> 0; -b/a; SE(b = 0; "Indeterminata; "Impossibile"))
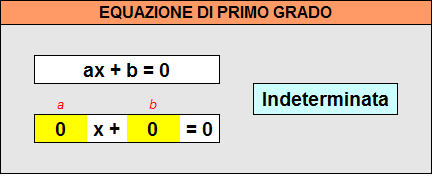
Il risultato dipende dal valore dell’espressione selezionata tra le 3 disponibili
- -b/a
- “Impossibile”
- “Indeterminata”
Soluzione 4
Puoi semplificare la formula precedente ma… avrai bisogno di
- una formula per ogni caso dell’equazione
- la funzione E().
Prova
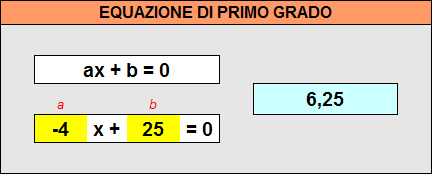
- (x0) = SE(E(a = 0; b <> 0); "Impossibile"; "---")
- (x1) = SE(a <> 0; -b/a; "---")
- (xi) = SE(E(a = 0; b = 0); "Indeterminata"; "---")