La funzione che associa a ogni valore x la probabilità che la variabile X assuma valori minori o uguali di x
- F(x) = p(X ≤ x)
- p(a < X ≤ b) = F(b) – F(a)
- a < b ⇒ F(a) ≤ F(b)
- 0 ≤ F(x) ≤ 1
Se x1 < x2 < … < xn
- x < x1 ⇒ F(x) = 0
- x ≥ xn ⇒ F(x) = 1
- xk ≤ x ≤ xk+1 ⇒ F(x) = p1 + p2 + … + pk
Teorema di Cebysev
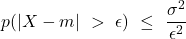
- La probabilità che lo scarto dalla media, in valore assoluto, sia maggiore di un valore prefissato è minore o uguale a …
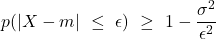
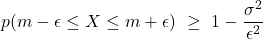
Esempi
- ε =σ
- p(|X-m| > σ) ≤ 1, inutile
- p(|X-m| ≤ σ) ≥ 0, inutile
- ε =2σ
- p(|X-m| > 2σ) ≤ 1/4 = 0,25
- p(|X-m| ≤ 2σ) ≥ 3/4 = 0,75
- ε =3σ
- p(|X-m| > 3σ) ≤ 1/9 = 0, 1111…, la probabilità che lo scarto tra il valore della variabile casuale e il suo valor medio superi il triplo della varianza è molto bassa
- p(|X-m| ≤ 3σ) ≥ 8/9 = 0,8888…, la probabilità che lo scarto tra il valore della variabile casuale e il suo valor medio non superi il triplo della varianza è molto alta