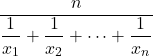Altre medie: troncata (spuntata), ponderata (pesata), quadratica, geometrica, armonica.
Media troncata
Media spuntata
- Prima si ordinano i valori
- poi si scartano i valori agli estremi dell’intervallo (in una certa percentuale)
- e infine si calcola la media aritmetica
Esempio
Dati 100 numeri, calcolare la media troncata al 10%
- ordina i 100 numeri
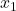 .
. 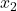 , …,
, …, 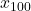
- scarta il 10% dei 100 numeri (i 5 più piccoli e i 5 più grandi) e rimangono…
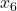 .
.  , …,
, …, 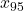
- calcola la media aritmetica dei 90 numeri rimasti
![]() =
= 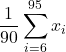 =
= ![]()
Media ponderata
Media pesata
Per calcolare la media ponderata di ![]() termini si calcola la somma di ogni valore moltiplicato per un certo peso e si divide per la somma dei pesi
termini si calcola la somma di ogni valore moltiplicato per un certo peso e si divide per la somma dei pesi
![]() =
= 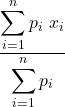 =
= ![]()
Se la somma dei pesi è 1,0 non è necessario dividere per la loro somma.
I pesi possono essere le frequenze
![]() =
= 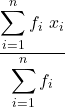 =
= ![]()
Media quadratica
La media quadratica di ![]() termini è la radice quadrata della media aritmetica dei quadrati dei valori:
termini è la radice quadrata della media aritmetica dei quadrati dei valori:
![]() =
= 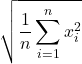 =
= ![]()
Media geometrica
La media geometrica di ![]() termini è la radice
termini è la radice ![]() -esima del prodotto degli
-esima del prodotto degli ![]() valori:
valori:
![]() =
= ![Rendered by QuickLaTeX.com \displaystyle \sqrt[{n}]{\prod _{i=1}^{n}x_{i}}](https://www.valcon.it/pp/wp-content/ql-cache/quicklatex.com-342833ab5ebd1705a3cc3d8dfeeb65c6_l3.png) =
= ![]()
Media armonica
La media armonica di ![]() termini è definita come il reciproco della media aritmetica dei reciproci:
termini è definita come il reciproco della media aritmetica dei reciproci:
![]() =
= 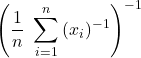 =
= 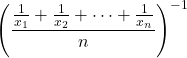 =
=