I test clinici sono soggetti a errore; a volte non rilevano una malattia in persone malate e a volte la rilevano in persone sane.
Una malattia colpisce il 2% delle persone di una popolazione.
Un test clinico risulta positivo, cioè rileva la malattia, nel 90% delle persone malate e nell’1% delle persone sane.
La situazione è descritta dal diagramma ad albero seguente.
Un individuo della popolazione si è sottoposto al test che è risultato positivo.
Qual è la probabilità che l’individuo sia malato?
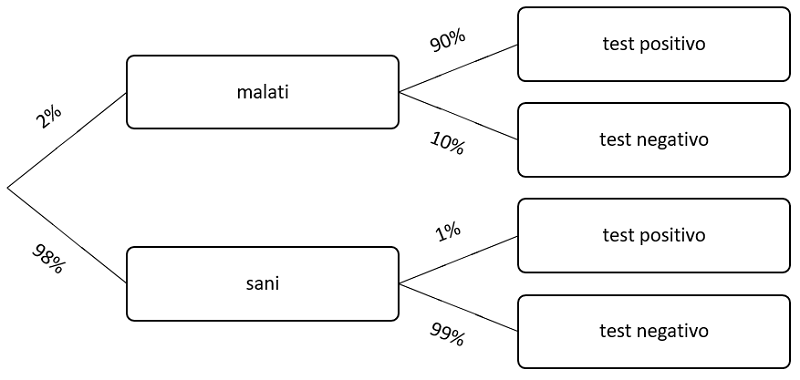
Sia
- M = individuo malato
- S = individuo sano
- P = test positivo
- N = test negativo
Un po’ di calcoli…
| ? | ||
|---|---|---|
| p(M) | = 2% | 2 persone su 100 sono malate |
| p(S) | = 98% | 98 persone su 100 sono sane |
| p(P | M) | = 90% | |
| p(N | M) | = 10% | Su 100 persona malate, 10 risultano negative |
| p(P | S) | = 1% | Su 100 persone sane, una risulta positiva |
| p(N | S) | = 99% | |
| p(M e P) | = p(M) · p(P | M) = 2% · 90% = 1,8% | Quasi 2 persone su 100 risultano positive al test e sono effettivamente malate |
| p(M e N) | = p(M) · p(N | M) = 2% · 10% = 0,2% | 2 persone su 1000 risultano negative al test ma sono malate… |
| p(S e N) | = p(S) · p(N | S) = 98% · 99% = 97,02% | Circa 97 persone su 100 risultano negative al test e sono effettivamente sane |
| p(S e P) | = p(S) · p(P | S) = 98% · 1% = 0,98% | Quasi una persona su 100 risulta positiva al test ma è sana… |
| p(P) | = p(M e P) + p(S e P) = 1,8% + 0,98% = 2,78% | Quasi 3 persone su 100 sono risultate positive al test |
| p(N) | = p(M e N) + p(S e N) = 0,2% + 97,02% = 97,22% | Circa 97 persone su 100 sono risultate negative al test |
| p(M | P) | = p(M e P) / p(P) = 1,8% / 2,78% ~ 64,75% | Meno di 2 persone su 3, tra quelle risultate positive, sono effettivamente malate! |
| p(S | P) | = p(S e P) / p(P) = 98% / 2,78% ~ 35,25% | Più di 1 persone su 3, tra quelle risultate positive, è sana! |
| p(M | N) | = p(M e N) / p(N) = 0,2% / 97,22% ~ 0,21% | Ogni 10.000 persone risultate negative ci sono circa 21 malate |
| p(S | N) | = p(S e N) / p(N) = 97,02% / 97,22% ~ 99,79% | Ogni 10.000 persone risultate negative ci sono circa 9.979 sane |
La probabilità che una persona risultata positiva al test sia effettivamente malata è del 64,75 %
Esercizio
- Organizza i dati in una tabella
- Poni che la popolazione sia di 10.000 persone
- Esplicita le frequenze assolute corrispondenti
| Persona malata | Persona sana | TOTALI | |||
|---|---|---|---|---|---|
| Test positivo | 2% * 90% = 1,8% | 180 | 98% * 1% = 0,98% | 98 | 278 |
| Test negativo | 2% * 10% = 0,2% | 20 | 98% * 99% = 97,02% | 9.702 | 9.722 |
| TOTALI | 1,8% + 0,2% = 2,0% | 200 | 0,98% + 97,02% = 98,0% | 9.800 | 10.000 |
| ? | ||
|---|---|---|
| p(M) | = 200 / 10.000 | 200 persone su 10.000 sono malate |
| p(M e P) | = 180 / 10.000 | 180 persone su 10.000 risultano positive al test e sono effettivamente malate |
| p(M e N) | = 20 / 10.000 | 20 persone su 10.000 risultano negative al test ma sono malate… |
| p(S) | = 9.800 / 10.000 | 9.800 persone su 10.000 sono sane |
| p(S e N) | = 9.702 / 10.000 | 9.702 persone su 10.000 risultano negative al test e sono effettivamente sane |
| p(S e P) | = 98 / 10.000 | 98 persone su 10.000 risultano positive al test ma sono sane |
| p(P) | = 278 / 10.000 | 278 persone su 10.000 sono risultate positive al test |
| p(M | P) | = 180 / 278 | Il 64,75 % delle persone risultate positive sono effettivamente malate! |
| p(N) | = 9.722 / 10.000 | 9.722 persone su 10.000 sono risultate negative al test |
| p(M | N) | = 20 / 9.722 | 20 persone tra le 9722 risultate negative in realtà sono malate! |