La torre di Hanoi

di

Il problema

Nel tempio di Brahma si trova una piattaforma di ottone con tre perni di diamanti.
Sul primo di tali perni sono infilati 64 dischi d’oro, di dimensioni decrescenti, che formano una torre.
Si deve portare la torre sul terzo perno, spostando un solo disco alla volta e in modo che mai un disco di diametro maggiore si trovi sopra un disco di diametro minore.
Per risolvere la questione si può utilizzare il secondo perno come perno di servizio.

Quando i monaci termineranno l’opera il mondo sarà finito!

Analisi

Siano D1, D2, …, Dn le etichette dei dischi di una torre di Hanoi con n dischi.

Il problema con un solo disco è banale

  1. sposta il disco D1 dalla 1° alla 3° torre


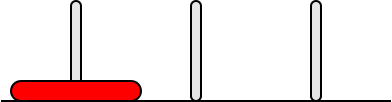
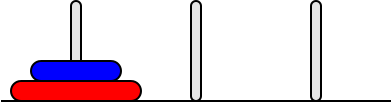
Se i dischi sono 2 le mosse sono 3

  1. sposta il disco D1 dalla 1° alla 2° torre
  2. sposta il disco D2 dalla 1° alla 3° torre
  3. sposta il disco D1 dalla 2° alla 3° torre


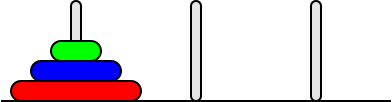
Se i dischi sono 3 le mosse sono 7

  1. sposta il disco D1 dalla 1° alla 3° torre
  2. sposta il disco D2 dalla 1° alla 2° torre
  3. sposta il disco D1 dalla 3° alla 2° torre
  4. sposta il disco D3 dalla 1° alla 3° torre
  5. sposta il disco D1 dalla 2° alla 1° torre
  6. sposta il disco D2 dalla 2° alla 3° torre
  7. sposta il disco D1 dalla 1° alla 3° torre


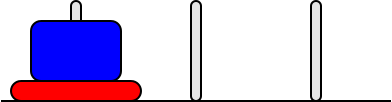
Se i dischi sono 4, 5, … si può riconoscere lo schema risolutivo

  1. sposta i dischi D1…Dn-1 dalla 1° alla 2° torre (usando la 3° come appoggio) in modo da liberare Dn
  2. sposta il disco Dn dalla 1° alla 3° torre
  3. sposta i dischi D1…Dn-1 dalla 2° alla 3° torre (usando la 1° come appoggio) sopra Dn


Algoritmo

Ad ogni passo è sufficiente specificare

  • il numero di dischi coinvolti, perché si parla sempre dei dischi in cima a una torre
  • il nome della torre di origine
  • il nome della torre di appoggio
  • il nome della torre di destinazione

allora l’algoritmo risolutivo per il problema

Hanoi(n, origine, appoggio, destinazione)

diventa

  1. Hanoi(n-1, origine, arrivo , appoggio)
  2. Hanoi(1, origine, appoggio, destinazione)
  3. Hanoi(n-1, appoggio, origine, destinazione)

con l’accortezza che nel caso di torre con un solo disco è sufficiente comunicare di spostare il disco dalla torre origine alla torre destinazione.