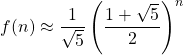Numeri di Fibonacci

I numeri di Fibonacci prendono il nome da una sfida matematica che Fibonacci lanciò a un suo collega.
Il problema tratta la proverbiale velocità con cui i conigli si riproducono:

il 1° mese è presente una coppia di conigli
una coppia di conigli diventa matura all’inizio del 2° mese di vita
la gestazione dura un mese
ogni parto produce una coppia maschio-femmina di conigli
ogni coppia di conigli sopravvive e si riproduce per sempre…

Calcolare il numero di coppie di conigli dopo 10 mesi.

Analisi

Tramite i pulsanti puoi osservare l’evoluzione della popolazione di conigli fino al sesto mese
Ogni mese sono presenti i conigli già presenti il mese precedente più quelli appena nati, che sono in numero uguale ai conigli presenti due mesi prima!

I numeri di Fibonacci sono proprio la successione 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, … cioè il numero di coppie di conigli per ogni mese.

Al decimo mese ci saranno 55 coppie di conigli.

Algoritmo iterativo

A partire dai valori noti (1, 1) si calcola, mese dopo mese, un nuovo valore finché non si giunge al mese richiesto.

Per calcolare fibonacci(5) si seguono i passi

fibonacci(1) = 1
fibonacci(2) = 1
fibonacci(3) = fibonacci(2) + fibonacci(1) = 1 + 1 = 2
fibonacci(4) = fibonacci(3) + fibonacci(2) = 2 + 1 = 3
fibonacci(5) = fibonacci(4) + fibonacci(3) = 3 + 2 = 5

Algoritmo ricorsivo

La formulazione ricorsiva dei numeri di Fibonacci è molto comoda perché sintetica ma…

$\displaystyle f(n)=\left \{ \begin{array}{ll} 1 & n=1,2 \\ f(n-1)+f(n-2) & n>2 \end{array}$

Per calcolare f(5) si seguono i passi

                      f(5)
                        |
           f(4) --------+--------f(3)
             |                     |
    f(3) ----+---- f(2)   f(2) ----+---- f(1)
      |              |      |              |
 f(2) + f(1)         1      1              1
   |      |
   1      1

Con formula!

Non è necessario alcun algoritmo iterativo o ricorsivo se si utilizza la formula

$\displaystyle f(n)=\frac{1}{\sqrt{5}}\left[\left(\frac{1+\sqrt{5}}{2}\right)^n-\left(\frac{1-\sqrt{5}}{2}\right)^n\right]$

Il contributo del secondo termine è così piccolo che può essere trascurato.
Calcola il primo termine e considera l’intero più vicino (arrotonda!)

$\displaystyle f(n) \approx \frac{1}{\sqrt{5}}\left(\frac{1+\sqrt{5}}{2}\right)^n$