Permutazioni con ripetizioni

La scrittura P_n;k significa

Le permutazioni di n simboli con un simbolo che si ripete k volte
Se un simbolo si ripete k volte le permutazioni si riducono di k! (Il numero di permutazioni dei k simboli uguali)
$\displaystyle P_{n;k} = \frac{n!}{k!}$
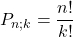
Quanti anagrammi si possono creare con n lettere se una si ripete k volte?
In generale, il coefficiente multinomiale
$\displaystyle P_{n;k1,k2,...} = \frac{P_n}{k_1! k_2! ...} = {n \choose k_1 k_2 ...}$

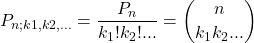
Prova a generare le permutazioni e contarle

Numero	Simboli	Permutazioni	Quantità
1	{A}	`A`	1
2	{A, A}	`AA`	1
	{A, B}	`AB BA`	2
3	{A, A, A}	`AAA`	1
	{A, A, B}	`AAB ABA BAA`	3
	{A, B, C}	`ABC ACB BAC BCA CAB CBA`	6
4	{A, A, A, A}	`AAAA`	1
	{A, A, A, B}	`AAAB AABA ABAA BAAA`	4
	{A, A, B, B}	`AABB ABAB ABBA BAAB BABA BBAA`	6
	{A, A, B, C}	`AABC AACB ABAC ABCA ACAB ACBA BAAC BACA BAAC CAAB CABA CBAA`	12
	{A, B, C, D}	`ABCD ABDC ACBD ACDB ADBC ADCB BACD BADC BCAD BCDA BDAC BDCA CABD CADB CBAD CBDA CDAB CDBA DABC DACB DBAC DBCA DCAB DCBA`	24
5	{A, A, A, A, A}	`AAAAAA`	1
	{A, A, A, A, B}	`AAAAB AAABA AABAA ABAAA BAAAA`	5
	{A, A, A, B, B}	`AAABB AABAB AABBA ABAAB ABABA ABBAA BAAAB BAABA BABAA BBAAA`	10
	{A, A, A, B, C}	`AAABC AAACB AABAC AABCA AACAB AACBA ABAAC ABACA ABCAA ACAAB ACABA ACBAA BAAAC BAACA BACAA BCAAA CAAAB CAABA CABAA CBAAA`	20
	{A, A, B, B, C}	`AABBC ...`	30
	{A, A, B, C, D}	`AABCD ...`	60
	{A, B, C, D, E}	`ABCDE ...`	120
6	{A, A, A, A, A, A}	`AAAAAA`	1
	{A, A, A, A, A, B}	`AAAAAB AAAABA AAABAA AABAAA ABAAAA BAAAAA`	6
	{A, A, A, A, B, B}	`AAAABB AAABAB AAABBA AABAAB AABABA AABBAA ABAAAB ABAABA ABABAA ABBAAA BAAAAB BAAABA BAABAA BABAAA BBAAAA`	15
	{A, A, A, A, B, C}	`AAAABC ...`	30
	{A, A, A, B, B, B}	`AAABBB ...`	20
	{A, A, A, B, B, C}	`AAABBC ...`	60
	{A, A, A, B, C, D}	`AAABCD ...`	120
	{A, A, B, B, C, C}	`AABBCC ...`	90
	{A, A, B, B, C, D}	`AABBCD ...`	180
	{A, A, B, C, D, E}	`AABCDE ...`	360
	{A, B, C, D, E, F}	`ABCDEF ...`	720

oppure calcola il loro numero con la formula degli anagrammi, coefficiente multinomiale

Numero	Simboli	Quantità
1	{A}	$\displaystyle \frac{1!}{1!}$	= 1
2	{A, A}	$\displaystyle \frac{2!}{2!}$	= 1
	{A, B}	$\displaystyle \frac{2!}{1!\cdot 1!}$	= 2
3	{A, A, A}	$\displaystyle \frac{3!}{3!}$	= 1
	{A, A, B}	$\displaystyle \frac{3!}{2!\cdot 1!}$	= 3
	{A, B, C}	$\displaystyle \frac{3!}{1!\cdot 1!\cdot 1!}$	= 6
4	{A, A, A, A}	$\displaystyle \frac{4!}{4!}$	= 1
	{A, A, A, B}	$\displaystyle \frac{4!}{3!\cdot 1!}$	= 4
	{A, A, B, B}	$\displaystyle \frac{4!}{2!\cdot 2!}$	= 6
	{A, A, B, C}	$\displaystyle \frac{4!}{2!\cdot 1!\cdot 1!}$	= 12
	{A, B, C, D}	$\displaystyle \frac{4!}{1!\cdot 1!\cdot 1!\cdot 1!}$	= 24
5	{A, A, A, A, A}	$\displaystyle \frac{5!}{5!}$	= 1
	{A, A, A, A, B}	$\displaystyle \frac{5!}{4!\cdot 1!}$	= 5
	{A, A, A, B, B}	$\displaystyle \frac{5!}{3!\cdot 2!}$	= 10
	{A, A, A, B, C}	$\displaystyle \frac{5!}{3!\cdot 1!\cdot 1!}$	= 20
	{A, A, B, B, C}	$\displaystyle \frac{5!}{2!\cdot 2!\cdot 1!}$	= 30
	{A, A, B, C, D}	$\displaystyle \frac{5!}{2!\cdot 1!\cdot 1!\cdot 1!}$	= 60
	{A, B, C, D, E}	$\displaystyle \frac{5!}{1!\cdot 1!\cdot 1!\cdot 1!\cdot 1!}$	= 120
6	{A, A, A, A, A, A}	$\displaystyle \frac{6!}{6!}$	= 1
	{A, A, A, A, A, B}	$\displaystyle \frac{6!}{5!\cdot 1!}$	= 6
	{A, A, A, A, B, B}	$\displaystyle \frac{6!}{4!\cdot 2!}$	= 15
	{A, A, A, A, B, C}	$\displaystyle \frac{6!}{4!\cdot 1!\cdot 1!}$	= 30
	{A, A, A, B, B, B}	$\displaystyle \frac{6!}{3!\cdot 3!}$	= 20
	{A, A, A, B, B, C}	$\displaystyle \frac{6!}{3!\cdot 2!\cdot 1!}$	= 60
	{A, A, A, B, C, D}	$\displaystyle \frac{6!}{3!\cdot 1!\cdot 1!\cdot 1!}$	= 120
	{A, A, B, B, C, C}	$\displaystyle \frac{6!}{2!\cdot 2!\cdot 2!}$	= 90
	{A, A, B, B, C, D}	$\displaystyle \frac{6!}{2!\cdot 2!\cdot 1!\cdot 1!}$	= 180
	{A, A, B, C, D, E}	$\displaystyle \frac{6!}{2!\cdot 1!\cdot 1!\cdot 1!\cdot 1!}$	= 360
	{A, B, C, D, E, F}	$\displaystyle \frac{6!}{1!\cdot 1!\cdot 1!\cdot 1!\cdot 1!\cdot 1!}$	= 720