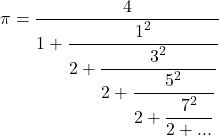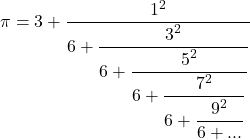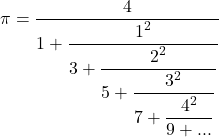Approssimazioni di pi greco

di
Pi greco

Frazioni

\displaystyle 3= \displaystyle 3
\displaystyle \left(\frac{16}{9}\right)^2= 3,\overline{160493827}
\displaystyle \frac{25}{8}= 3,125
\displaystyle \frac{142}{45}= 3,1\overline{5}
\displaystyle \frac{157}{50}= 3,14
\displaystyle \frac{22}{7}= 3,\overline{142857}Archimede
\displaystyle \frac{377}{120}= 3,141\overline{6}
\displaystyle \frac{211875}{67441}= 3,14163...
\displaystyle \frac{62832}{20000}= 3,1416
\displaystyle \frac{355}{113}= 3,1415929...Zu Chongzhi
……
\displaystyle \pi= 3,141592653589793...

Radici

\displaystyle \sqrt{10}= 3,162277660...
\displaystyle \sqrt[3]{31}= 3,141380652...
\displaystyle \sqrt[5]{306}= 3,1415522358...
\displaystyle \sqrt{\frac{227}{23}}= 3,141586417...
\displaystyle \sqrt[6]{\frac{17305}{18}}= 3,1415924876...
\displaystyle \sqrt[4]{\frac{2143}{22}}= 3,14159265...
……
\displaystyle\pi= 3,141592653589793…

Serie

Pi greco può essere catturato ricorrendo a infinite addizioni

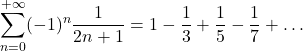\displaystyle \frac{\pi}{4}=\displaystyle \sum_{n=0}^{+\infty}(-1)^n \frac{1}{2n+1}=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\dotsLeibniz: reciproci dei numeri dispari, con segni alterni
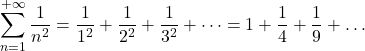\displaystyle \frac{\ \pi^2}{6}=\displaystyle \sum_{n=1}^{+\infty}\frac{1}{n^2}=\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\dots=1+\frac{1}{4}+\frac{1}{9}+\dotsEulero: reciproci dei quadrati
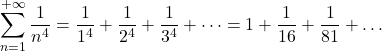\displaystyle \frac{\ \pi^4}{90}=\displaystyle \sum_{n=1}^{+\infty}\frac{1}{n^4}=\frac{1}{1^4}+\frac{1}{2^4}+\frac{1}{3^4}+\dots=1+\frac{1}{16}+\frac{1}{81}+\dotsReciproci delle quarte potenze
\displaystyle \pi=\displaystyle 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}-\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}+\frac{1}{9}-\frac{1}{10}+\frac{1}{11}+\frac{1}{12}-\frac{1}{13}+\dotsIl numero 2 ha segno positivo
I numeri primi della forma (4m-1) hanno segno positivo
I numeri primi della forma (4m+1) hanno segno negativo
Per i numeri composti il segno è il prodotto dei segni dei singoli fattori
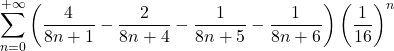\displaystyle \pi=\displaystyle \sum_{n=0}^{+\infty} \left(\frac{4}{8n+1}-\frac{2}{8n+4}-\frac{1}{8n+5}-\frac{1}{8n+6}\right) \left(\frac{1}{16}\right)^nBailey, Borwein, Plouffe
…
\displaystyle \frac {1}{\pi }}=\displaystyle {\frac {2{\sqrt {2}}}{9801}}\sum _{{n=0}}^{\infty }{\frac {(4n)!(1103+26390n)}{(n!)^{4}396^{{4n}}}}Ramanujan
…

Produttorie

Pi greco può essere catturato ricorrendo a infinite moltiplicazioni

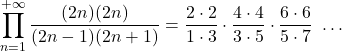\displaystyle \frac{\pi}{2}=\displaystyle \prod_{n=1}^{+\infty}\frac{(2n)(2n)}{(2n-1)(2n+1)}=\frac{2\cdot 2}{1\cdot 3}\cdot \frac{4\cdot 4}{3\cdot 5}\cdot \frac{6\cdot 6}{5\cdot 7} \ \dotsWallis: al numeratore tutti i quadrati dei numeri pari,
al denominatore i prodotti …
\displaystyle \frac{\pi}{4}=\displaystyle \frac{3}{4}\cdot\frac{5}{4}\cdot\frac{7}{8}\cdot\frac{11}{12}\cdot\frac{13}{12}\cdot\frac{17}{16}\cdot\frac{19}{20}\cdot\frac{23}{24}\ \dotsEulero: al numeratore tutti i numeri primi dispari,
al denominatore il multiplo di 4 più vicino al numeratore
\displaystyle \frac{\ \pi ^2}{6}=\displaystyle \frac{1}{\left(1-\frac{1}{2^2} \right)}\cdot \frac{1}{\left(1-\frac{1}{3^2} \right)}\cdot \frac{1}{\left(1-\frac{1}{5^2} \right)}\dotsEulero: il prodotto percorre tutti i numeri primi
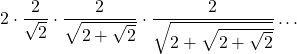\displaystyle \pi=\displaystyle 2 \cdot \frac{2}{\sqrt{2}} \cdot \frac{2}{\sqrt{2+\sqrt{2}}} \cdot \frac{2}{\sqrt{2+\sqrt{2+\sqrt{2}}}}\dotsViète
…
………

Frazioni continue

Pi greco può essere catturato ricorrendo a infinite divisioni (frazioni)

\displaystyle \pi = \frac{4}{\displaystyle 1+\frac{1^2}{\displaystyle 2+\frac{3^2}{\displaystyle 2+\frac{5^2}{\displaystyle 2+\frac{7^2}{\displaystyle 2+...}}}}}}

\displaystyle \pi =3+ \frac{1^2}{\displaystyle 6+\frac{3^2}{\displaystyle 6+\frac{5^2}{\displaystyle 6+\frac{7^2}{\displaystyle 6+\frac{9^2}{\displaystyle 6+...}}}}}}

\displaystyle \pi = \frac{4}{\displaystyle 1+\frac{1^2}{\displaystyle 3+\frac{2^2}{\displaystyle 5+\frac{3^2}{\displaystyle 7+\frac{4^2}{\displaystyle 9+...}}}}}}