Osserva
- Il primo poligono è un quadrato
- Il valore di
 è necessario per il passo successivo
è necessario per il passo successivo - Il poligono successivo ha il doppio dei lati del precedente
Lato | Perimetro | Pi greco | Apotema | Delta | |
|---|---|---|---|---|---|
| 4 | 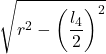 | ||||
| 8 | 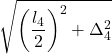 | 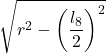 | |||
| 16 | 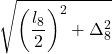 | 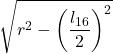 |
- Sostituendo il valore
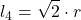
Lato | Perimetro | Pi greco | Apotema | Delta | |
|---|---|---|---|---|---|
| 4 | |||||
| 8 | |||||
| 16 | 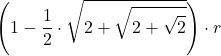 |
- L’approssimazione di
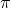 non dipende da
non dipende da 
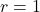
Lato | Perimetro | Pi greco | Apotema | Delta | |
|---|---|---|---|---|---|
| 4 | |||||
| 8 | |||||
| 16 | |||||
| 32 | 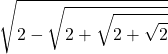 | 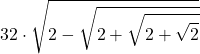 | 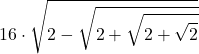 | 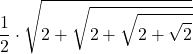 | 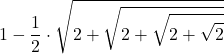 |
Approssimazioni
Osserva le approssimazioni successive di pi greco e una forma equivalente (produttoria di Viète)
| Passo | #Lati | |||
|---|---|---|---|---|
| 1 | 4 | 2,82842712474619 | ||
| 2 | 8 | 3,06146745892072 | ||
| 3 | 16 | 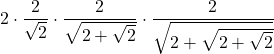 | 3,12144515225805 | |
| 4 | 32 | 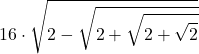 | … | 3,13654849054594 |
| 5 | 64 | 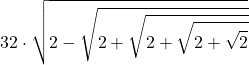 | … | 3,14033115695475 |
| 6 | 128 | 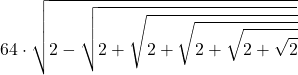 | … | 3,14127725093277 |
| 7 | 256 | … | … | 3,1415138011443 |
| 8 | 512 | … | … | 3,14157294036709 |
| 9 | 1024 | … | … | 3,14158772527716 |
| 10 | 2048 | … | … | 3,1415914215112 |
| … | … | … | … | … |
Approfondimenti
- Wikipedia: Metodo di esaustione
- Liu Hui, Zu Chongzhi