Pi greco con metodo geometrico

Pi greco

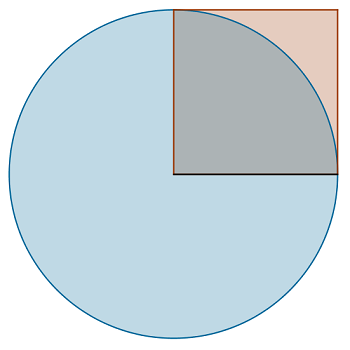
Considera un cerchio di raggio unitario con centro nell’origine.
Sapendo che l’area di uno dei 4 settori circolari è $\pi / 4$ calcola un valore approssimato di pi greco utilizzando uno dei metodi di integrazione di tipo geometrico.

Osserva

$r = 1$
$\displaystyle A_4 = \frac{\pi}{4}$
$\displaystyle \pi = 4\cdot A_4$
$x \in [0, 1]$
$\displaystyle f(x)=\sqrt{1-x^2}$

Segui i passi

decidi in quante parti dividere l’intervallo di integrazione
calcola il passo corrispondente per le ascisse
calcola le ordinate corrispondenti
scegli il metodo da utilizzare (rettangoli, trapezi, parabole)
calcola l’approssimazione di pi greco corrispondente

Calcoli

Approssimazioni di pi greco

n	Rettangoli Sinistra	Rettangoli Centro	Rettangoli Destra	Trapezi	Parabole
1	4,0	3,4641…	0	2,0
2	3,732…	3,259…	1,732…	2,732…	2,976…
3	3,58422…	3,2064…	2,25…	2,91755…
4	3,4957…	3,1839…	2,4957…	2,9957…	3,08…
5	3,437…	…	2,637…	…
6	3,3953…	…	2,7286…	…	…
…	…	…	…	…	…
100	3,160417…	3,1419…	3,12…	3,140417…	…