Linear Congruential Generator
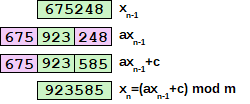
Osserva: xn=(axn-1+c) mod m
- Il prodotto per a (1001) produce un numero con più cifre ma con le cifre più significative e le cifre meno significative piuttosto prevedibili
- Il contributo di c (337) permette di mescolare le cifre meno significative
- L’operazione finale di modulo m (1000000) scarta le cifre più significative
Si ottiene il massimo periodo (m) se
- c e m sono primi tra loro
c (337) non ha divisori in comune con m (1000000) - Se p è un fattore primo di m deve esserlo anche di a-1
2 e 5 sono i fattori primi di m (1000000) e sono anche fattori primi di a-1 (1000) - Se 4 divide m allora deve dividere anche a-1
4 divide m (1000000) e divide anche a-1 (1000)
Esempi
| m | p|m | 4|m | a (1 … m-1) | c (1 … m-1) |
|---|---|---|---|---|
| 40 | 2 5 | 4 | 20n+1 1 21 | 1 3 7 9 11 13 17 19 21 23 27 29 31 33 37 39 |
| 90 | 2 3 5 | 30n+1 1 31 61 | 1 7 11 13 17 19 23 29 31 37 41 43 47 49 53 59 61 67 71 73 77 79 83 89 | |
| 100 | 2 5 | 4 | 20n+1 1 21 41 61 81 | 1 3 7 9 11 13 17 19 21 23 27 29 31 33 37 39 41 43 47 49 51 53 57 59 61 63 67 69 71 73 77 79 81 83 87 89 91 93 97 99 |
| 121 | 11 | 11n+1 1 12 23 34 45 56 67 78 89 100 111 | 1 2 3 4 5 6 7 8 9 10 12 13 14 15 16 17 18 19 20 21 23 24 25 26 27 28 29 30 31 32 34 35 36 37 38 39 40 41 42 43 45 46 47 48 49 50 51 52 53 54 56 57 58 59 60 61 62 63 64 65 67 68 69 70 71 72 73 74 75 76 78 79 80 81 82 83 84 85 86 87 89 90 91 92 93 94 95 96 97 98 100 101 102 103 104 105 106 107 108 109 111 112 113 114 115 116 117 118 119 120 | |
| 128 | 2 | 4 | 4n+1 1 5 9 13 17 21 25 29 33 37 41 45 49 53 57 61 65 69 73 77 81 85 89 93 97 101 105 109 113 117 121 125 | 1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49 51 53 55 57 59 61 63 65 67 69 71 73 75 77 79 81 83 85 87 89 91 93 95 97 99 101 103 105 107 109 111 113 115 117 119 121 123 125 127 |