QUESITI sulle Carte da gioco

di

INVALSI
O.I.I.
Test

INVALSI – II – 2014/15 – 6

Da un mazzo di 52 carte da gioco (composto da 13 carte per ognuno dei semi: cuori, quadri, fiori, picche) sono stati tolti i 4 assi.
Si estrae una carta a caso.
Qual è la probabilità che sia di cuori?

Da un mazzo di 52 carte uguale al precedente sono state tolte alcune carte di fiori.
Dopo questa operazione la probabilità di estrarre, a caso, una carta di fiori è 6/45.
Quante carte di fiori sono state tolte?

SOLUZIONE

Carte tolteMazzo di cartep(♥)
 1♥…K♥
1♦…K♦
1♣…K♣
1♠…K♠		\displaystyle \frac{13}{52} = \displaystyle \frac{1}{4}
1♥
1♦
1♣
1♠		2♥…K♥
2♦…K♦
2♣…K♣
2♠…K♠		\displaystyle \frac{12}{48} = \displaystyle \frac{1}{4}
Carte tolteMazzo di cartep(♣)
 1♥…K♥
1♦…K♦
1♣…K♣
1♠…K♠		\displaystyle \frac{13}{52}
1♣1♥…K♥
1♦…K♦
2♣…K♣
1♠…K♠		\displaystyle \frac{12}{51}
1♣2♣1♥…K♥
1♦…K♦
3♣…K♣
1♠…K♠		\displaystyle \frac{11}{50}
1♣…3♣1♥…K♥
1♦…K♦
4♣…K♣
1♠…K♠		\displaystyle \frac{10}{49}
1♣…4♣1♥…K♥
1♦…K♦
5♣…K♣
1♠…K♠		\displaystyle \frac{9}{48}
1♣… 5♣1♥…K♥
1♦…K♦
6♣…K♣
1♠…K♠		\displaystyle \frac{8}{47}
1♣…6♣1♥…K♥
1♦…K♦
7♣…K♣
1♠…K♠		\displaystyle \frac{7}{46}
1♣…7♣1♥…K♥
1♦…K♦
8♣…K♣
1♠…K♠		\displaystyle \frac{6}{45}

Oppure

\displaystyle \frac{13-x}{52-x} = \displaystyle \frac{6}{45}

…

x = 7

OII 18-11-2015 – 5

Gelsomina, la nonna di Francesco, decide di proporre al nipote un gioco di carte.
Crea un mazzo formato da 4 re (K), 4 donne (Q) e 4 fanti (J), le mescola bene bene e distribuisce le 12 carte coperte in fila.

Poi ne scopre 4, nel seguente modo:

Quindi dice a Francesco che, secondo lei:

  1. la probabilità che la prima carta sia un fante è del 25%
  2. la probabilità che la penultima carta sia una donna è del 25%
  3. la probabilità che la penultima carta sia un re è del 37,5%
  4. è più probabile che la terza carta sia un re che un fante.

Ma nonna Gelsomina sta segretamente interrogando Francesco in matematica, dietro consiglio della figlia Gardenia, e ha detto una cosa falsa.

SOLUZIONE

Tenendo conto del numero di carte rimaste e del numero di posizioni disponibili si possono calcolare le probabilità e verificare le affermazioni

\displaystyle p_1 = \frac{2}{8} = 0,25 = 25%, vero

\displaystyle p_2 = \frac{3}{8} = 0,375 = 37,5%, falso

\displaystyle p_3 = \frac{3}{8} = 0,375 = 37,5%, vero

p_1 > p_3, vero

Risposta: L’affermazione (2) è falsa.

OII 16-11-2017 – 2

Si supponga di avere un mazzo di carte francesi (52 carte, con semi: cuori, quadri, fiori, picche).
Si supponga di prendere una carta C1 dal mazzo, di rimetterla dentro, mischiare, prenderne una seconda C2, rimetterla dentro, mischiare e prendere una terza carta C3.

Qual è la probabilità che C1, C2 e C3 siano tutte e tre carte di cuori?

SOLUZIONE

p(C1 è cuori e C2 è cuori e C3 è cuori)
= p(C1 è cuori) • p(C2 è cuori) • p(C3 è cuori)
= 1/4 • 1/4 • 1/4
= 1/64

OIS 2018 – IV Eliminatorie – 18

Sia dato un mazzo di 52 carte da gioco e i seguenti eventi:

  • A = “estrazione di un asso”;
  • B = “estrazione di una carta rossa (ovvero di cuori o di quadri)”;
  • C = “estrazione di un figura”.

Quale delle seguenti affermazioni è falsa?

Scegli un’alternativa:

  1. La probabilità che si verifichino simultaneamente sia A che C è nulla
  2. La probabilità che si verifichino simultaneamente sia B che C è diversa da zero
  3. La probabilità dell’evento A è più bassa della probabilità dell’evento C
  4. La probabilità che si verifichino simultaneamente sia A che B è nulla
  5. Non so

Concorso 2012 – 2618

Qual è la probabilità di estrarre da un mazzo di 52 carte da gioco un re o una carta di cuori?

1/13 | 4/13 | 17/52 | 1/4

SOLUZIONE

  • Eventi: {1♥…K♥, 1♦…K♦, 1♣…K♣, 1♠…K♠}
  • Numero eventi = 52
  • Eventi favorevoli: {1♥…K♥} ∪ {K♥, K♦, K♣, K♠} = {1♥…K♥, K♦, K♣, K♠}
  • Numero eventi favorevoli = 16
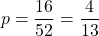  • \displaystyle p=\frac{16}{52}=\frac{4}{13} = 0,30769… = 30,769…%

Concorso 2012 – 2736

Qual è la probabilità di estrarre da un mazzo di 52 carte da gioco una carta che non sia di cuori?

Soluzione 1

  • Eventi: {1♥…K♥, 1♦…K♦, 1♣,…,K♣, 1♠,…,K♠}
  • Numero eventi = 52
  • Eventi favorevoli: {1♦…K♦, 1♣,…,K♣, 1♠,…,K♠}
  • Numero eventi favorevoli = 39
  • p(…) = 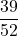\displaystyle \frac{39}{52} = \displaystyle \frac{3}{4} = 0,75 = 75%

Soluzione 2

Considera prima la probabilità di estrarre una carta di cuori

  • Eventi: {1♥…K♥, 1♦…K♦, 1♣…K♣, 1♠…K♠}
  • Numero eventi = 52
  • Eventi favorevoli: {1♥…K♥}
  • Numero eventi favorevoli = 13
  • p(“cuori”) = \displaystyle \frac{13}{52} = \displaystyle \frac{1}{4}
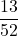  • p(…) = 1-p(“cuori”) = 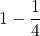\displaystyle 1-\frac{1}{4} = \displaystyle \frac{3}{4} = 0,75 = 75%

Calcolare la probabilità di estrarre di seguito tre carte di cuori da un mazzo di 52, considerando che le carte possono essere solo di quattro semi: cuori, picche, fiori e quadri.

Due carte vengono estratte a caso da un mazzo di 52 carte.
Qual è la probabilità che siano entrambe di picche.

Estraiamo a caso una carta da un mazzo di 52 carte da gioco.
Qual è la probabilità che la carta estratta sia di fiori oppure sia una figura?

Nella seguente situazione di gioco effettuato con un mazzo di 40 carte si estrae una carte…

Nel seguente gioco due giocatori estraggono una carta dal mazzo…

Si supponga di avere un mazzo di carte francesi (52 carte, con semi: cuori, quadri, fiori, picche).
Si supponga di prendere una carta C1 dal mazzo, di rimetterla dentro, mischiare, prenderne una seconda C2, rimetterla dentro, mischiare e prendere una terza carta C3.
Qual è la probabilità che C1, C2 e C3 siano tutte e tre carte di cuori?

Un giocatore di briscola riceve in mano tre carte di un mazzo da 40.
Qual è la probabilità che il giocatore abbia in mano almeno un asso?