QUESITI sulla Teoria dei giochi

Tratto dal libro di testo

Supponiamo di lanciare un dado a 6 facce e di puntare sul 6.

Se ripetiamo il lancio 6000 volte quante volte uscirà la faccia numero 6?
Scommettendo 1€ per 600 giocate, con una vincita di 3€, quale sarà il bilancio finale?
Qual è la speranza matematica del gioco?

SOLUZIONE

Probabilità del numero 6: $\displaystyle \frac{1}{6}$

Per la legge empirica del caso: $\displaystyle \frac{1}{6}\cdot 6000$ = 1000

Scommettendo 1€ si vince 3€ ma si riceve 2€, per la legge empirica del caso

~ 2€ • $\displaystyle \frac{1}{6}\cdot 600$ = +200€

Scommettendo 1€ si perde 1€, per la legge empirica del caso

~ -1€ • $\displaystyle \frac{5}{6}\cdot 600$ = -500€

Il bilancio finale sarà:

~ 2€ • $\displaystyle \frac{1}{6}\cdot 600$ – 1€ • $\displaystyle \frac{5}{6}\cdot 600$ = … = -300€

Speranza matematica:

$\displaystyle 2\cdot \frac{1}{6} - 1\cdot \frac{5}{6}$ = $\displaystyle -\frac{3}{6}$ = -0,5 = -50%

Tratto dal libro di testo

Nel seguente gioco due giocatori estraggono una carta dal mazzo:

Il primo giocatore vince 3 € se esce una carta di fiori e vince 5 € se esce una carte di picche
Il secondo giocatore vince 4 € se esce una carta rossa

Il gioco è equo?

SOLUZIONE

Numero carte: 52
Numero carte di fiori: 13
Numero carte di picche: 13
Numero carte rosse (cuori e quadri): 13+13 = 26
Numero carte nere (fiori e picche): 13+13 = 26
p(“picche”) = 13/52
p(“fiori”) = 13/52
p(“rossa”) = 26/52
p(“nera”) = 26/52

Speranza matematica 1° giocatore:

$\displaystyle +3\cdot \frac{13}{52}+5\cdot \frac{13}{52}-4\cdot \frac{26}{52}$ = … = 0

Speranza matematica 2° giocatore:

$\displaystyle -3\cdot\frac{13}{52}-5\cdot\frac{13}{52}+4\cdot\frac{26}{52}$ = … = 0

Il gioco è equo.

Tratto dal libro di testo

Nella seguente situazione di gioco effettuato con un mazzo di 40 carte si estrae una carte:

se è una figura vinci 0,70 €
se non è una figura ma è una carta di bastoni o spade vinci 0,50 €
se è il settebello perdi 16 €.

Rispondi

Qual è la speranza matematica del gioco?
Dopo molte giocate chi ne trae vantaggio?
Come devono cambiare le regole affinché il gioco divenga equo?

SOLUZIONE

Numero carte = 40
Numero figure = 12
Numero bastoni o spade = 20
Numero bastoni o spade senza figure = 14
Numero settebello = 1
p(“figura”) = 12/40
p(“bastoni o spade, no figura”) = 14/40
p(“settebello”) = 1/40

Speranza matematica giocatore

E1 = $\displaystyle +0,7\cdot\frac{12}{40}+0,5\cdot\frac{14}{40}-16\cdot\frac{1}{40}$ = … = -0,015 (-1,5%)

Speranza matematica mazziere

E2 = $\displaystyle -0,7\cdot\frac{12}{40}-0,5\cdot\frac{14}{40}+16\cdot\frac{1}{40}$ = … = +0,015 (+1,5%)

Il gioco è favorevole per il mazziere

Diventa equo, per esempio, se la prima vincita è 0,75 €

E1 = $\displaystyle +0,75\cdot\frac{12}{40}+0,5\cdot\frac{14}{40}-16\cdot\frac{1}{40}$ = … = 0
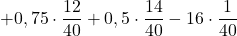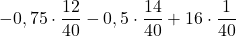E2 = $\displaystyle -0,75\cdot\frac{12}{40}-0,5\cdot\frac{14}{40}+16\cdot\frac{1}{40}$ = … = 0

Partecipi ad un gioco che ha due varianti: in entrambe lanci due dadi, ma nella prima vinci se i due dadi mostrano la stessa faccia, mentre nella seconda se la somma delle due facce è pari a 7.

Di due diverse lotterie sono stati venduti, rispettivamente, 400 e 350 biglietti.
Avendo acquistato 15 biglietti della prima e 18 biglietti della seconda, in quale delle due lotterie si ha la maggior probabilità di vincere?

A quale delle due varianti del gioco preferisci partecipare?

Alla prima
Alla seconda
Ritieni che siano equivalenti
Gli esiti delle due varianti del gioco non sono confrontabili

Carnival Game

Il gioco di fine millennio

Calcola la speranza matematica del numero secco al Lotto sapendo che si gioca con 5 numeri estratti su 90 e che in caso di vittoria il banco paga 11,232 volte la giocata.