Radice cubica

di
Radici e zeri

< 1.000

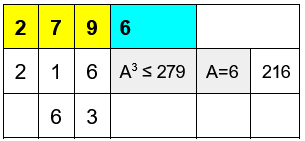
La radica cubica di un numero abc, minore di 1000, è un numero A (con una cifra) tale che

(A)^3 = abc

Cerca a tentativi il numero A minore di 10 il cui cubo sia minore, o uguale, di abc

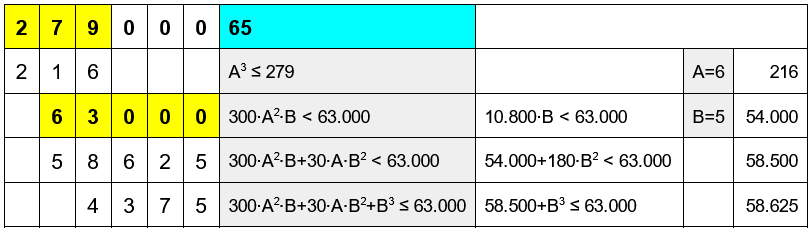
Prova con 279 (= 6^3 + 63)

< 1.000.000

La radica cubica di un numero abcdef, minore di 1.000.000, è un numero AB (con 2 cifre) tale che

(AB)^3 = abcdef

(AB)^3 = (A\cdot 10+B)^3

= A^3\cdot 1.000+3\cdot A^2\cdot 100 \cdot B+3\cdot A\cdot 10 \cdot B^2 + B^3

= 1.000\cdot A^3+300\cdot A^2\cdot B+30\cdot A\cdot B^2 + B^3

Osserva

  • La prima cifra della soluzione, A, è tale che il suo cubo non superi il valore abc
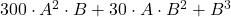  • La seconda cifra della soluzione, B, è tale che 300\cdot A^2\cdot B+30\cdot A\cdot B^2 + B^3 non superi il valore rimanente
  • Calcola solamente 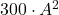300\cdot A^2 e determina B tale che…
  • Calcola 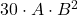30\cdot A\cdot B^2 e controlla se…
  • Calcola 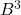B^3 e controlla se…

Prova con 279.000 (= 65^3 + 4.375)

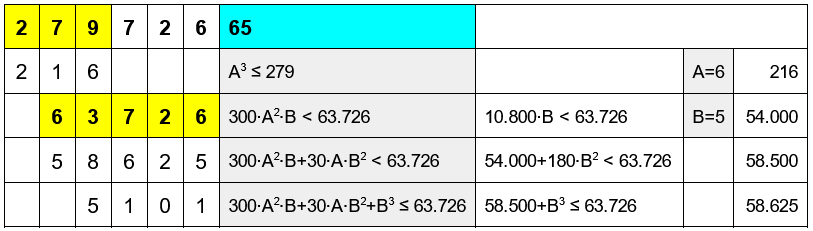
Prova con 279.726 (= 65^3 + 5.101)

< 1.000.000.000

La radica cubica di un numero abcdefghi, minore di 1.000.000.000, è un numero ABC (con 3 cifre) tale che

(ABC)^3 = abcdefghi

(ABC)^3 = (AB\cdot 10 + C)^3

= (AB)^3\cdot 1.000+3\cdot (AB)^2\cdot 100 \cdot C+3\cdot AB\cdot 10 \cdot C^2 + C^3

= 1.000 \cdot (AB)^3+300\cdot (AB)^2\cdot C+30\cdot AB\cdot C^2 + C^3

Osserva

  • Per passare dalle due cifre AB alle tre cifre ABC bisogna ripetere il passo precedente con AB al posto di A e C al posto di B…

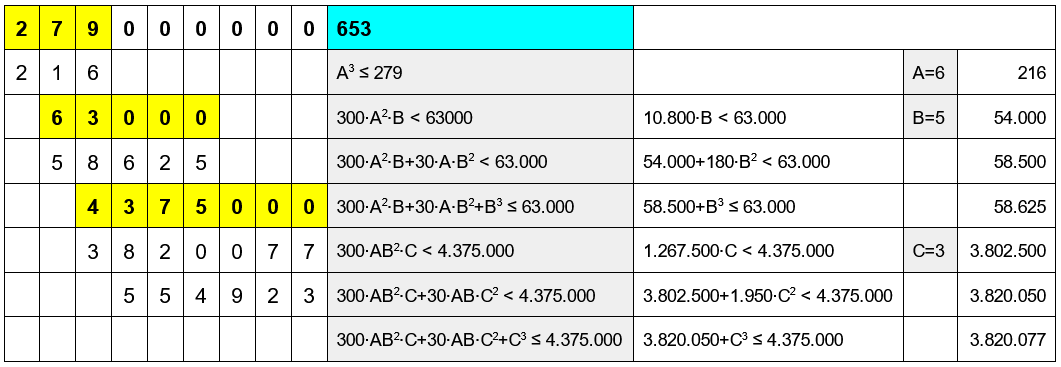
Prova con 279.000.000 (= 653^3 + 554.923)

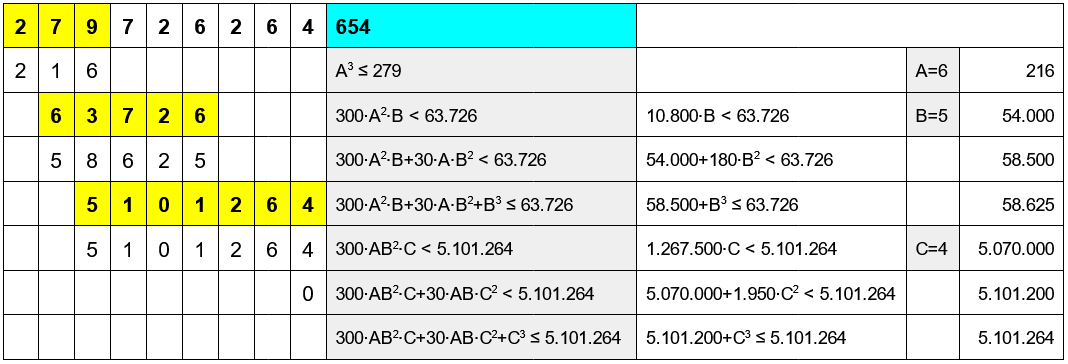
Prova con 279.726.264 (= 654^3)

Riepilogo

  • \displaystyle \sqrt[3]{279} = 6 e resto=63
  • \displaystyle \sqrt[3]{279.000} = 65 e resto 4.375
  • \displaystyle \sqrt[3]{279.726} = 65 e resto 5.101
  • \displaystyle \sqrt[3]{279.000.000} = 653 e resto 554.923
  • \displaystyle \sqrt[3]{279.726.264} = 654 e resto 0 (cubo perfetto)

Ma allora…

\displaystyle \sqrt[3]{279}\displaystyle \sqrt[3]{279}\displaystyle \sqrt[3]{279}
= \displaystyle \frac{1}{10}\sqrt[3]{10^3 \cdot 279}= \displaystyle \frac{1}{100}\sqrt[3]{100^3 \cdot 279}= \displaystyle \frac{1}{1000}\sqrt[3]{1000^3 \cdot 279}
= \displaystyle \frac{1}{10}\sqrt[3]{279.000}= \displaystyle \frac{1}{100}\sqrt[3]{279.000.000}…
= \displaystyle \frac{1}{10}\sqrt[3]{65^3 + 4.375}= \displaystyle \frac{1}{100}\sqrt[3]{653^3 + 554.923}…
= \displaystyle \frac{1}{10}\sqrt[3]{10^3 \cdot ((6,5)^3\ + 4,375)}= \displaystyle \frac{1}{100}\sqrt[3]{100^3 \cdot ((6,53)^3\ + 0,554923)}…
= \displaystyle \frac{1}{10}\cdot 10\ \sqrt[3]{(6,5)^3 + 4,375}= \displaystyle \frac{1}{100}\cdot 100\ \sqrt[3]{(6,53)^3 + 0,554923}…
= 6,5
con resto 4,375		= 6,53
con resto 0,554923		= 6,534
con resto 0,042918696

Algoritmo

  1. Dividi le cifre in gruppi da 3 partendo da destra
  2. La prima cifra, A, si individua provando con le 3° potenze dei numeri da 1 a 9 …
  3. Dalla seconda cifra in poi, B, C…, si moltiplica il quadrato del risultato parziale per 300 e …
  4. Se il risultato non è esatto (se il numero non è un cubo perfetto) si può individuare una cifra decimale aggiuntiva aggiungendo 3 zeri, e così via…