Metodo scolastico

di
Radici e zeri

< 100

La radica quadrata di un numero ab, minore di 100, è un numero A (con una cifra) tale che

(A)^2 = ab

Cerca a tentativi il numero A minore di 10 il cui quadrato sia minore, o uguale, di ab

Prova con 42 (= 6^2 + 6)

< 10.000

La radica quadrata di un numero abcd, minore di 10.000, è un numero AB (con 2 cifre) tale che

(AB)^2 = abcd

(AB)^2 = (A\cdot 10+B)^2

= A^2\cdot 100+2\cdot A\cdot B\cdot 10+B^2

= A^2\cdot 100+(20\cdot A+B)\cdot B

Osserva

  • La prima cifra della soluzione, 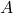A, è tale che il suo quadrato non superi il valore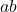 ab
  • La seconda cifra della soluzione, 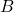B, è tale che il valore dell’espressione 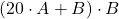(20\cdot A+B)\cdot B non superi il valore rimanente

Prova con 4.200 (= 64^2 + 104)

Prova con 4.277 (= 65^2 + 52)

< 1.000.000

La radica quadrata di un numero abcdef, minore di 1.000.000, è un numero ABC (con 3 cifre) tale che

(ABC)^2 = abcdef

(ABC)^2 = ((AB)\cdot 10 +C)^2

= (AB)^2\cdot 100 + 2\cdot (AB)\cdot 10 \cdot C +C^2

= 100\cdot (AB)^2 + (20\cdot (AB) +C) \cdot C

Osserva

  • La fattorizzazione è simile alla precedente,,,
  • AB ha preso il posto di A e C ha preso il posto di B

Prova con 420.000 (= 648^2 + 96)

Prova con 427.716 (= 654^2)

Riepilogo

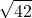  • \displaystyle \sqrt{42} = 6 e resto 6
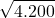  • \displaystyle \sqrt{4.200} = 64 e resto 104
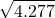  • \displaystyle \sqrt{4.277} = 65 e resto 52
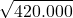  • \displaystyle \sqrt{420.000} = 648 e resto 96
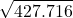  • \displaystyle \sqrt{427.716} = 654 e resto 0 (quadrato perfetto)

Le cifre dopo la virgola?

Per calcolare le cifre dopo la virgola

  • aggiungi due zeri al valore iniziale (moltiplichi per 100) e calcoli la prima cifra esatta dopo la virgola
  • aggiungi ancora due zeri (moltiplichi ancora per 100) e calcoli la seconda cifra esatta dopo la virgola
  • …

Algoritmo?

Dato un numero intero positivo o nullo calcola le cifre intere esatte della sua radice quadrata

  1. Dividi le cifre in coppie partendo da destra verso sinistra.
  2. La prima cifra della soluzione è tale che il suo quadrato non superi la prima coppia (o singola cifra).
  3. Sottrai il suo quadrato
  4. Per tutte le cifre successive
    • abbassa due cifre (se le cifre sono finite aggiungi due zeri)
    • moltiplica per 20 la soluzione parziale, S
    • individua il valore della x nell’espressione 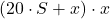(20\cdot S+x)\cdot x che non superi il valore attuale
    • sottrai…

Perché funziona con le cifre dopo la virgola?

\displaystyle \sqrt{42}= \displaystyle \frac{1}{10}\sqrt{10^2\cdot 42}= \displaystyle \frac{1}{10}\sqrt{4.200}= \displaystyle \frac{1}{10}\sqrt{64^2 + 104}
= \displaystyle \frac{1}{10}\sqrt{10^2\cdot ((6,4)^2 + 1,04)}= \displaystyle \frac{1}{10}\cdot 10\ \sqrt{(6,4)^2 + 1,04}= 6,4
r=1,04
\displaystyle \sqrt{42}= \displaystyle \frac{1}{100}\sqrt{100^2\cdot 42}= \displaystyle \frac{1}{100}\sqrt{420.000}= \displaystyle \frac{1}{100}\sqrt{648^2 + 96}
= \displaystyle \frac{1}{100}\sqrt{100^2\cdot ((6,48)^2 + 0,0096)}= \displaystyle \frac{1}{100}\cdot 100\ \sqrt{(6,48)^2 + 0,0096}= 6,48
r=0,0096
\displaystyle \sqrt{42}= \displaystyle \frac{1}{1000}\sqrt{1000^2\cdot 42}= \displaystyle \frac{1}{1000}\sqrt{42.000.000}= \displaystyle \frac{1}{1000}\sqrt{6480^2 + 9600}
= \displaystyle \frac{1}{1000}\sqrt{1000^2\cdot ((6,480)^2 + 0,0096)}= \displaystyle \frac{1}{1000}\cdot 1000\ \sqrt{(6,480)^2 + 0,0096}= 6,480
r=0,0096
\displaystyle \sqrt{42}………
……= 6,4807
r= 0,00052751

Quindi: 42 = (6)2 + 6 = (6,4)2 + 1,04 = (6,48)2 + 0,0096 = (6,480)2 + 0,0096 = (6,4807)2 + 0,00052751 = …

RISORSE