Problemino di Katia: come deve essere prolungata la seguente sequenza?
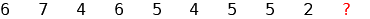
Si tratta di un esercizio in un testo di scuola media!
Soluzione 1
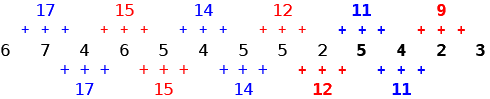
Sequenza: 6, 7, 4, 6, 5, 4, 5, 5, 2, 5, 4, 2, 3, …
Le somme di tre numeri consecutivi sono uguali a coppie e le somme sono decrescenti con la regola -2, -1, -2, -1, …
Soluzione 1 bis
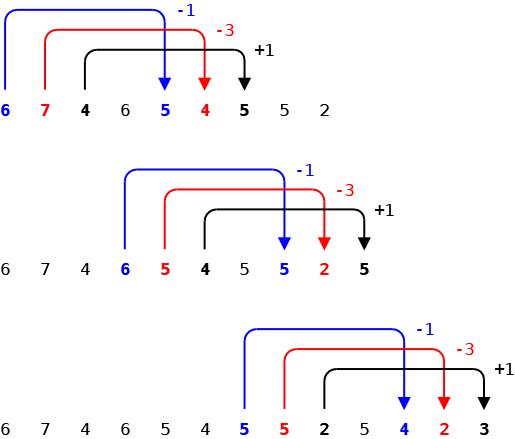
Sequenza: 6, 7, 4, 6, 5, 4, 5, 5, 2, 5, 4, 2, 3, …
Dalla 5° posizione in poi il valore dipende da quello di 4 posizioni precedenti, secondo la regola ripetuta -1, -3, +1
Soluzione 2
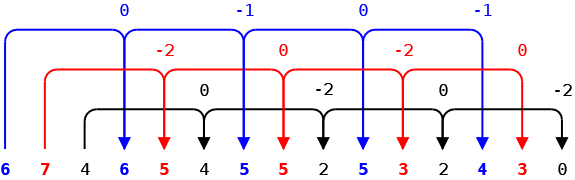
Sequenza: 6, 7, 4, 6, 5, 4, 5, 5, 2, 5, 3, 2, 4, 3, 0, …
Tre sequenze indipendenti di coppie decrescenti con variazione -1,-2,-2
Soluzione 3
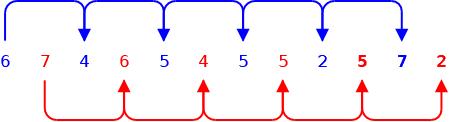
Sequenza: 6, 7, 4, 6, 5, 4, 5, 5, 2, 5, 7, 2, 6, 7, 4, 6, 5, 4, 5, 5, 2, …
Una sequenza 7, 6, 4, 5, 5, 2 che si ripete alternata con se stessa
Soluzione 4
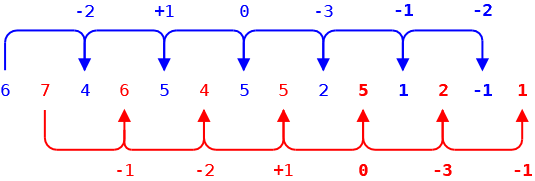
Sequenza: 6, 7, 4, 6, 5, 4, 5, 5, 2, 5, 1, 2, -1, 1, …
Una sequenza con variazioni -1, -2, +1, 0, -3 alternata con se stessa
Soluzione 5
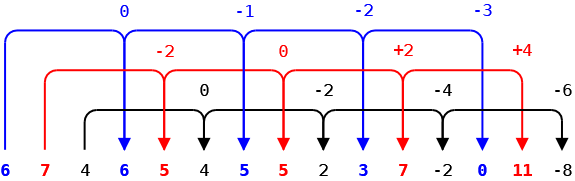
Sequenza: 6, 7, 4, 6, 5, 4, 5, 5, 2, 3, 7, -2, 0, 11, -8, …
Tre sequenze indipendenti e le loro variazioni sono progressioni aritmetiche con ragione -1, +2, -2
Conclusioni
- Nel libro di testo l’esercizio segue immediatamente un esempio simile risolto…
- Per ogni sequenza (di lunghezza qualsiasi…) esistono infinite sequenze che la prolungano ragionevolmente!
- La soluzione è data dalla sequenza che risulta più VEROSIMILE nel contesto culturale di chi propone il quesito e di chi deve risolverlo.