Sistemi lineari, con la regola di Cramer

di
Algebra lineare

Risolvere un sistema lineare (2 equazioni, 2 variabili)

\begin{cases}ax+by=e \\ cx+dy=f\end{cases}

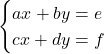
Utilizzando uno dei metodi disponibili (sostituzione, confronto, …) si arriva alla soluzione (se ad-bc\ne 0)

\begin{cases} \displaystyle x=\frac{de-bf}{ad-bc} \\ \displaystyle y=\frac{af-ce}{ad-bc} \end{cases}

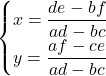
Sono necessari un certo numero di passaggi e le formule finali sono di difficile memorizzazione.

L’algoritmo di Cramer è semplice da ricordare e da applicare… ma richiede la capacità di calcolare il determinante di una matrice

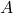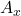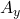  • Considera la matrice dei coefficienti del sistema A e le matrici A_x e A_y con la colonna dei termini noti al posto di quella di x e di y, rispettivamente
  • Calcola i 3 determinanti corrispondenti
  • Le formule precedenti per x e y possono essere espresse in modo più immediato
MatriciDeterminantiSoluzione
A = \displaystyle \begin{bmatrix} a & b \\ c & d \end{bmatrix}|A| = \displaystyle \begin{vmatrix} a & b \\ c & d \end{vmatrix} = a d - b c
A_x = \displaystyle \begin{bmatrix} e & b \\ f & d \end{bmatrix}|A_x| = \displaystyle \begin{vmatrix} e & b \\ f & d \end{vmatrix} = d e - b fx = \displaystyle \frac{|A_x|}{|A|}
A_y = \displaystyle \begin{bmatrix} a & e \\ c & f \end{bmatrix}|A_y| = \displaystyle \begin{vmatrix} a & e \\ c & f \end{vmatrix} = a f - c ey = \displaystyle \frac{|A_y|}{|A|}

Considera delle matrici generiche 2×2, 3×3, 4×4, …

MatriciDeterminantiSoluzione
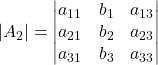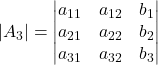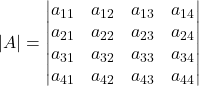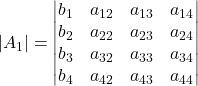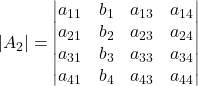\displaystyle A = \begin{bmatrix}a_{11} & a_{12}\\a_{21} & a_{22} \end{bmatrix}\displaystyle |A| = \begin{vmatrix}a_{11} & a_{12}\\a_{21} & a_{22} \end{vmatrix}
\displaystyle |A_1| = \begin{vmatrix}b_1 & a_{12} \\b_2 & a_{22}\end{vmatrix}x_1 = \displaystyle \frac{|A_1|}{|A|}
\displaystyle |A_2| = \begin{vmatrix}a_{11} & b_1 \\a_{21} & b_2\end{vmatrix}x_2 = \displaystyle \frac{|A_2|}{|A|}
\displaystyle A = \begin{bmatrix}a_{11} & a_{12} & a_{13} \\a_{21} & a_{22} & a_{23} \\a_{31} & a_{32} & a_{33} \end{bmatrix}\displaystyle |A| = \begin{vmatrix}a_{11} & a_{12} & a_{13} \\a_{21} & a_{22} & a_{23} \\a_{31} & a_{32} & a_{33} \end{vmatrix}
\displaystyle |A_1| = \begin{vmatrix}b_1 & a_{12} & a_{13} \\b_2 & a_{22} & a_{23} \\b_3 & a_{32} & a_{33} \end{vmatrix}x_1 = \displaystyle \frac{|A_1|}{|A|}
\displaystyle |A_2| = \begin{vmatrix}a_{11} & b_1 & a_{13} \\a_{21} & b_2 & a_{23} \\a_{31} & b_3 & a_{33} \end{vmatrix}x_2 = \displaystyle \frac{|A_2|}{|A|}
\displaystyle |A_3| = \begin{vmatrix}a_{11} & a_{12} & b_1\\a_{21} & a_{22} & b_2 \\a_{31} & a_{32} & b_3 \end{vmatrix}x_3 = \displaystyle \frac{|A_3|}{|A|}
\displaystyle A = \begin{bmatrix}a_{11} & a_{12} & a_{13} & a_{14}\\a_{21} & a_{22} & a_{23} & a_{24}\\a_{31} & a_{32} & a_{33} & a_{34}\\a_{41} & a_{42} & a_{43} & a_{44}\end{bmatrix}\displaystyle |A| = \begin{vmatrix}a_{11} & a_{12} & a_{13} & a_{14}\\a_{21} & a_{22} & a_{23} & a_{24}\\a_{31} & a_{32} & a_{33} & a_{34}\\a_{41} & a_{42} & a_{43} & a_{44} \end{vmatrix}
\displaystyle |A_1| = \begin{vmatrix}b_{1} & a_{12} & a_{13} & a_{14}\\b_{2} & a_{22} & a_{23} & a_{24}\\b_{3} & a_{32} & a_{33} & a_{34}\\b_{4} & a_{42} & a_{43} & a_{44} \end{vmatrix}x_1 = \displaystyle \frac{|A_1|}{|A|}
\displaystyle |A_2| = \begin{vmatrix}a_{11} & b_{1} & a_{13} & a_{14}\\a_{21} & b_{2} & a_{23} & a_{24}\\a_{31} & b_{3} & a_{33} & a_{34}\\a_{41} & b_{4} & a_{43} & a_{44} \end{vmatrix}x_2 = \displaystyle \frac{|A_2|}{|A|}
\displaystyle |A_3| = \begin{vmatrix}a_{11} & a_{12} & b_{1} & a_{14}\\a_{21} & a_{22} & b_{2} & a_{24}\\a_{31} & a_{32} & b_{3} & a_{34}\\a_{41} & a_{42} & b_{4} & a_{44} \end{vmatrix}x_3 = \displaystyle \frac{|A_3|}{|A|}
\displaystyle |A_4| = \begin{vmatrix}a_{11} & a_{12} & a_{13} & b_{1}\\a_{21} & a_{22} & a_{23} & b_{2}\\a_{31} & a_{32} & a_{33} & b_{3}\\a_{41} & a_{42} & a_{43} & b_{4} \end{vmatrix}x_4 = \displaystyle \frac{|A_4|}{|A|}