Teoria dei giochi – ValCon.It

Gioco d’azzardo

Il giocatore partecipa per ottenere un guadagno in denaro ma la sua vincita (perdita) è determinata esclusivamente (o quasi) dal caso e non dalle sue abilità

Legge empirica del caso

In una serie di prove ripetute un gran numero di volte nelle stesse condizioni, ciascuno degli eventi possibili si manifesta con una frequenza relativa che è circa uguale alla sua probabilità.

Legge dei grandi numeri

Teorema di Bernoulli: al crescere di n diventa sempre meno probabile osservare valori di frequenze relative che differiscono molto da p.

Speranza matematica

V, variabile casuale discreta che assume i valori delle vincite in un gioco, v₁, v₂, …, v_n, che si verificano con probabilità p₁, p₂, …, p_n
la speranza matematica di V è il valore medio di V
- M(V) = p₁v₁ + p₂v₂ + … + p_nv_n = $\displaystyle \sum_i p_i \ v_i$
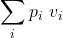
- M(V) = 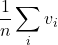$\displaystyle \frac{1}{n} \sum_i v_i$ , la media aritmetica delle vincite per un gran numero di partite…

Siano

c, prezzo per giocare
V, variabile casuale discreta vincita lorda
V-c, variabile casuale discreta vincita netta
$M(V-c) = M(V) - c$

La speranza matematica (vincita netta) per alcuni giochi

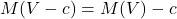
Gioco equo	La speranza matematica della vincita lorda è uguale al prezzo da pagare	La speranza matematica della vincita netta di ogni giocatore è 0
	$M(V)=c$	$M(V-c)=0$
Gioco favorevole per il giocatore	La speranza matematica della vincita lorda è maggiore del costo da pagare	La speranza matematica della vincita netta è positiva
	$M(V)>c$	$M(V-c)>0$
Gioco sfavorevole per il giocatore	La speranza matematica della vincita lorda è minore del costo da pagare	La speranza matematica della vincita netta è negativa
	$M(V)<c$	$M(V-c)<0$