Biagio, l’allenatore della squadra di pallavolo di Vattelapesca, ha letto nel suo manuale del perfetto allenatore di pallavolo la seguente regola: in ogni momento in campo devono giocare un alzatore, due schiacciatori e tre universali.
Nella squadra sono disponibili complessivamente dieci giocatori, e, precisamente
- 2 alzatori
- 3 schiacciatori
- 5 universali.
Sapendo che un giocatore non può cambiare ruolo (ad esempio un alzatore non potrà giocare come schiacciatore o universale) quante diverse formazioni può schierare Biagio utilizzando i suoi dieci giocatori e rispettando la regola d’oro del suo manuale del perfetto allenatore?
Soluzione: 60.
Soluzione 1
Con i giocatori a disposizione è possibile combinare le seguenti sottosquadre
+------------+-----------------+--------------+
| 1 alzatore | 2 schiacciatori | 3 universali |
| su 2 | su 3 | su 5 |
+------------+-----------------+--------------+
| a1 | s1-s2 | u1-u2-u3 |
| a2 | s1-s3 | u1-u2-u4 |
| | s2-s3 | u1-u2-u5 |
| | | u1-u3-u4 |
| | | u1-u3-u5 |
| | | u1-u4-u5 |
| | | u2-u3-u4 |
| | | u2-u3-u5 |
| | | u2-u4-u5 |
| | | u3-u4-u5 |
+------------+-----------------+--------------+
| 2 | 3 | 10 |
+------------+-----------------+--------------+
e quindi le squadre
+-----------------------+-----------------------+-----+-----------------------+
| 1 | 2 | ... | 10 |
+---+-----------------------+-----------------------+-----+-----------------------+
| 1 | a1 + s1-s2 + u1-u2-u3 | a1 + s1-s2 + u1-u2-u4 | ... | a1 + s1-s2 + u3-u4-u5 |
| 2 | a1 + s1-s3 + u1-u2-u3 | a1 + s1-s3 + u1-u2-u4 | ... | a1 + s1-s3 + u3-u4-u5 |
| 3 | a1 + s2-s3 + u1-u2-u3 | a1 + s2-s3 + u1-u2-u4 | ... | a1 + s2-s3 + u3-u4-u5 |
+---+-----------------------+-----------------------+-----+-----------------------+
| 1 | a2 + s1-s2 + u1-u2-u3 | a2 + s1-s2 + u1-u2-u4 | ... | a2 + s1-s2 + u3-u4-u5 |
| 2 | a2 + s1-s3 + u1-u2-u3 | a2 + s1-s3 + u1-u2-u4 | ... | a2 + s1-s3 + u3-u4-u5 |
| 3 | a2 + s2-s3 + u1-u2-u3 | a2 + s2-s3 + u1-u2-u4 | ... | a2 + s2-s3 + u3-u4-u5 |
+---+-----------------------+-----------------------+-----+-----------------------+
Per un totale di 2*3*10 = 60 combinazioni
Soluzione 2
Osserva
- numero scelte per 1 saltatore su 2:
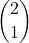 = 2
= 2 - numero scelte per 2 schiacciatori su 3:
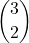 = 3
= 3 - numero scelte per 3 universali su 5:
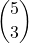 = 10
= 10
e le formazioni disponibili sono
![]() = 2 · 3 · 10 = 60.
= 2 · 3 · 10 = 60.