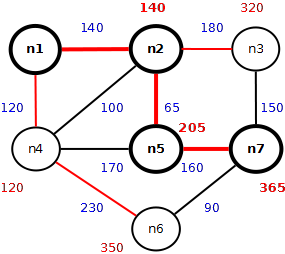
Il grafo dei collegamenti bidirezionali fra 7 nodi (n1, n2, …, n7) è descritto da una tabella
+-------+-------+-----+ | Nodo1 | nodo2 | km | +-------+-------+-----+ | n1 | n2 | 140 | | n2 | n3 | 180 | | n2 | n4 | 100 | | n1 | n4 | 120 | | n2 | n5 | 65 | | n4 | n5 | 170 | | n4 | n6 | 230 | | n3 | n7 | 150 | | n5 | n7 | 160 | | n7 | n6 | 90 | +-------+-------+-----+
Trovare la lista L del percorso più breve dal nodo n1 al nodo n7 e calcolarne la distanza D in chilometri.
1
Disegno il grafo corrispondente alla tabella e individuo la soluzione passo-passo.
I calcoli potrebero essere svolti semplicemente consultando la tabella ma i grafi semplificano il lavoro…
2
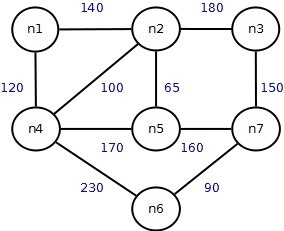
Distanze minime tra n1 e le città immediatamente vicine (n2 e n4)
- n1 -> n2 = 140
- n1 -> n4 = 120
3
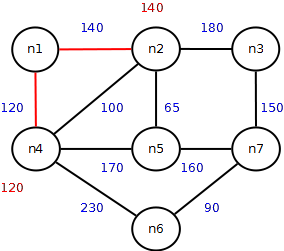
Distanze minime tra n1 e le città immediatamente vicine a n2 e n4 (n3, n5, n6)
- n1 -> n2 = 140
- n1 -> n2 -> n3= 320
- n1 -> n4 = 120
- n1 -> n2 -> n4= 240, scartata
- n1 -> n2 -> n5= 205
- n1 -> n4 -> n5= 290, scartata
- n1 -> n4 -> n6 = 350
4
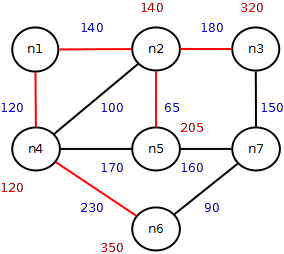
Distanza minima tra n1 e la città immediatamente vicina a n3, n5, n6 (n7)
- n1 -> n2 = 140
- n1 -> n2 -> n3= 320
- n1 -> n4 = 120
- n1 -> n2 -> n5= 205
- n1 -> n4 -> n6 = 350
- n1 -> n2 -> n5 -> n7 = 365
- n1 -> n2 -> n3 -> n7 = 470, scartata
- n1 -> n4 -> n6 -> n7 = 440, scartata
Soluzione: L=[n1, n2, n5, n7], D=365.