1

Si consideri una scacchiera di dimensione 6×6.
Qual è il massimo numero di scacchiere 3×3 che ci sono nella scacchiera?
- 4
- 24
- 16
- 12
2
Il prodotto di tre numeri interi e positivi è 300.
Se uno dei tre numeri è 5, qual è il valore minimo della somma degli altri due?
- 16
- 19
- 32
- 23
3
Un numero palindromo è un numero che produce la stessa sequenza di cifre sia che venga letto da sinistra verso destra sia da destra verso sinistra.
Per esempio, 6374554736 e 14741 sono numeri palindromi.
Quanti numeri palindromi ci sono tra 100 e 1000?
- 80
- 100
- 9
- 90
SOLUZIONE
- Il primo numero palindromo nell’intervallo è 101
- L’ultimo numero palindromo nell’intervallo è 999
- La prima è la terza cifra sono uguali e il valore può essere qualsiasi da 1 a 9
- La seconda cifra può essere qualsiasi valore da 0 a 9
- Le combinazioni possibili sono 9·10 = 90
4
Individuare quale tra i seguenti diagrammi soddisfa la relazione insiemistica esistente fra i termini seguenti:
- laureato in giurisprudenza
- avvocato
- sciatore

5
Due treni partono dalla stessa stazione ferroviaria nello stesso istante, uno verso est alla velocità di 60 Km/h l’altro verso ovest alla velocità di 80 Km/h.
Dopo quanto tempo disteranno l’uno dall’altro 350 Km?
- 1h e 30 min
- 2 h
- 2 h e 30 min
- 2 h e 50 min.
13
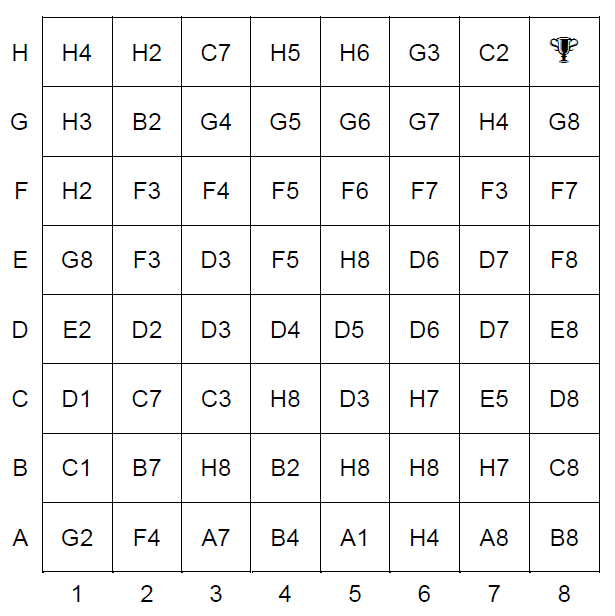
Un campo di gara per robot ha la forma di un foglio a quadretti o celle; ogni cella contiene le coordinate di un’altra cella, che è dove dovrà andare il robot.
Per esempio, se il robot entra nella cella G1, da qui dovrà spostarsi nella cella H3, e da qui dovrà poi andare nella cella C7.
C’è un tesoro nella cella H8, e il robot può partire da una qualsiasi cella della fila A (ovvero A1…A8).
Qual è il numero di celle NUMT, della fila A, che conducono al tesoro?
Contando anche la casella iniziale e la casella del tesoro, quale è il numero minimo MINT di caselle del percorso più breve che il robot può fare per arrivare al tesoro, e quale è il numero massimo MAXT di caselle del percorso più lungo per arrivare al tesoro?
(Si contano come visitate solo le caselle in cui il robot si ferma e legge le coordinate della cella successiva in cui spostarsi, non contano le caselle in cui il robot transita di passaggio).
14
Per descrivere un algoritmo, possiamo utilizzare uno pseudo-linguaggio di programmazione, dove il simbolo ← rappresenta l’istruzione che impone di “assegnare al nome simbolico che lo precede il valore calcolato dall’espressione che lo segue” (per esempio: x ← x + 1 significa “incrementa di 1 il valore associato al nome simbolico x e associa a x il valore incrementato”.
Se a x era associato il valore 5, dopo l’esecuzione dell’istruzione a x sarà associato il valore 6).
In questa ipotesi, scegliere la “condizione1” e la “condizione2” mancanti nel seguente algoritmo in modo che risolva nel minor tempo possibile la verifica del fatto che un numero intero n >= 0 letto da tastiera sia primo oppure no:
leggi da tastiera n p ← VERO i ← 2 finché "condizione1" AND "condizione2" è vera esegui ripetutamente da qui r ← resto di n diviso i se (r = 0) allora p ← FALSO i ← i + 1 a qui scrivi su video se (p è VERO) “Il numero n è primo” altrimenti “Il numero n non è primo”
- condizione1:
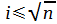
condizione 2: p FALSO - condizione1:
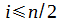
condizione 2: p VERO - condizione1:
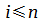
condizione 2: p FALSO - condizione1:
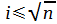
condizione 2: p VERO
15
Quattro gondole A, B, C e D sono ormeggiate sulla riva sinistra di un canale.
Un gondoliere deve portare le quattro gondole sulla riva destra.
Essendo di differente grandezza, le gondole impiegano tempi diversi per attraversare il canale: La gondola A impiega 2 minuti, la gondola B 4 minuti, la gondola C 8 minuti e la gondola D 16 minuti.
Il gondoliere può condurre una sola gondola alla volta, ma può agganciare alla gondola su cui si trova una seconda gondola e trainarla, impiegando in questo caso il tempo di quella più lenta.
Qual è il tempo minimo necessario al gondoliere per trasferire le 4 gondole da una riva all’altra?
- 32 minuti
- 30 minuti
- 60 minuti
- 24 minuti
16 <–
La grafica della tartaruga prevede che si possano impartire degli ordini di movimento a una tartaruga, che li eseguirà lasciando sul terreno una traccia dei suoi movimenti, come se avesse una penna attaccata sulla pancia.
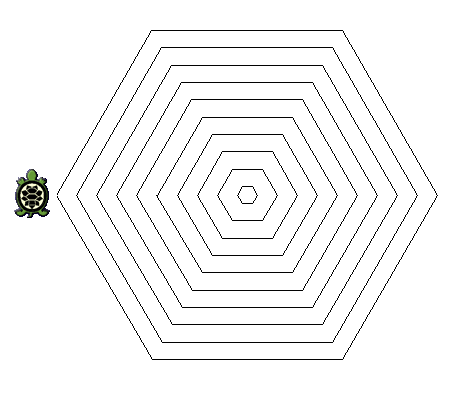
Gli ordini possono essere impartiti tramite un semplice linguaggio, stando attenti che:
- le istruzioni destra e sinistra sono relative all’orientamento attuale della tartaruga, e il numero che segue è un angolo espresso in gradi;
- pennasu e pennagiu sollevano e abbassano rispettivamente la penna sotto la pancia della tartaruga: quando la penna è sollevata ovviamente non lascia tracce sul terreno;
- l’istruzione ripeti fa ripetere il blocco che segue, delimitato da parentesi graffe, per un numero di volte indicato a fianco dell’istruzione.
Data la seguente figura prodotta con la grafica della tartaruga e il seguente codice che l’ha prodotta, indicare quali numeri mancano nelle posizioni indicate dalle lettere X, Y e Z
lato = 10
ripeti 10
{
pennagiu
destra 30
ripeti --- X ---
{
avanti lato
destra 60
}
pennasu
sinistra --- Y ---
avanti --- Z ---
destra 90
lato = lato + 20
}
17
In una scacchiera 3×3 ci sono inizialmente due cavalli neri negli angoli in alto e due cavalli bianchi negli angoli in basso, come mostrato nella parte sinistra della figura qui sopra sotto.

Qual è il numero minimo NMIN di mosse per scambiare i cavalli, ovvero avere i due cavalli neri in basso e i due cavalli bianchi in alto?
I cavalli, secondo le regole degli scacchi, si muovono con la loro tipica mossa ad ‘L’ (tre passi in totale, di cui uno o due in verticale o in orizzontale e i restanti in una direzione perpendicolare) e non ci possono essere due cavalli nella stessa posizione.
[Problema di Paolo Guerini da Forlì, 1512]
18 <–
Consideriamo il seguente algoritmo, che prende in ingresso un intero positivo N:
- Se N vale 1, l’algoritmo termina.
- Se N è pari, dividi N per 2, altrimenti (se N è dispari) moltiplicalo per 3 e aggiungi 1.
Per esempio, applicato al valore N = 6, l’algoritmo produce la seguente sequenza (di lunghezza 9, contando anche il valore iniziale N = 6 e il valore finale 1): 6, 3, 10, 5, 16, 8, 4, 2, 1.
La congettura di Collatz, chiamata anche congettura 3N+1, afferma che l’algoritmo qui sopra termini sempre per qualsiasi valore N; in altre parole, se prendo un qualsiasi numero intero maggiore di 1, applicare la regola numero 2 conduce sempre al numero 1.
Considerando i numeri compresi tra 10 e 20 (estremi inclusi), qual è tra questi il numero NUM la cui lunghezza LUN della sequenza, calcolata usando l’algoritmo descritto qui sopra, è la minore?
19
Il grafo in figura rappresenta una rete di trasporti tra le città c1, …, c6.
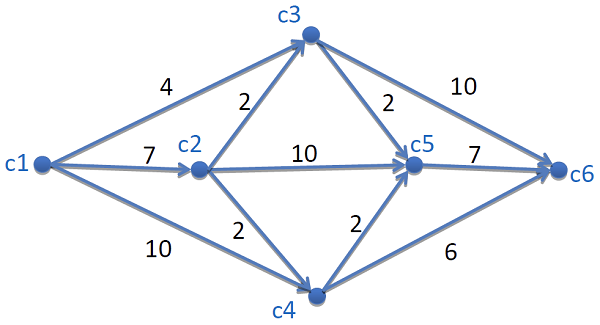
Ogni freccia tra due città è etichettata dal valore massimo di passeggeri che è possibile trasportare tra le due città.
I passeggeri possono anche essere divisi tra una città e l’altra; ad esempio, se mandiamo sette passeggeri tra c1 e c2, questi poi possono essere divisi a piacere, rispettando il valore massimo: uno può andare a c3, quattro a c5 e i restanti due a c4.
Qual è il valore massimo NUMPAS di passeggeri che è possibile far viaggiare da c1 a c6?
20
Ci sono 7 abitazioni, rappresentate dalle lettere da A a G, collegate da strade.
Si vuole realizzare un sistema di videosorveglianza, installando telecamere nelle case, in maniera tale che tutte le strade siano “coperte”: una telecamera installata in una casa è in grado di coprire tutte le strade collegate a quella casa.
Ad esempio, nella figura qui sotto, mettere una telecamera nella casa B copre le tre strade (A,B), (B,C) e (B,D).
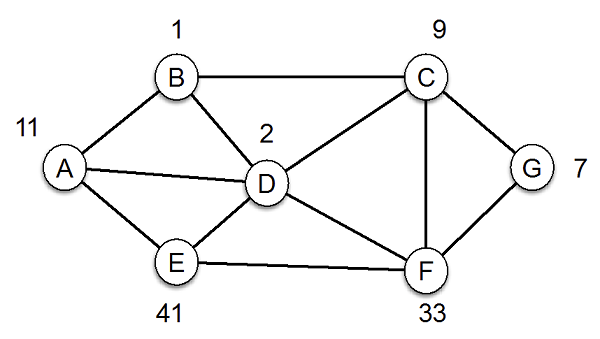
Sapendo che i numeri rappresentano il costo di installare la telecamera nella casa (quindi, ad esempio, mettere la telecamera nella casa A costa 11, nella casa D costa 2), qual è il costo minimo CMIN per coprire tutte le strade?
Nota: è possibile montare le telecamere in entrambe le case agli estremi di una stessa strada.
Ad esempio, è possibile coprire tutte le strade mettendo le telecamere nelle case {A, B, C, E, F, G}, per un costo totale di 102 (ma ovviamente questa non è la soluzione minima).