Dei numeri 1, 2, 3, …, 6000, quanti non sono divisibili né per 2, né per 3, né per 5?
Soluzione 1
Utilizza la forza bruta
- Scrivi i numeri da 1 a 6000
- Elimina i multipli di 2
- Elimina i multipli di 3
- Elimina i multipli di 5
- Conta i numeri rimanenti.
 Soluzione 2
Soluzione 2
Ricorda che
- Se
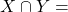 allora
allora 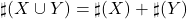
altrimenti
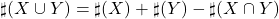
- Se
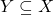 allora
allora 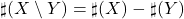
altrimenti
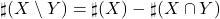
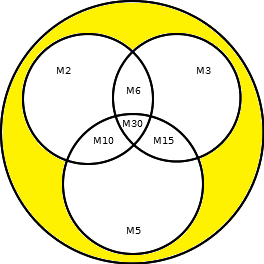
Osserva l’immagine a destra e considera che
M2 ∪ M3 ∪ M5 = M2 ∪ M3 ∪ M5 \ M6 \ M10 \ M15 ∪ M30
e di conseguenza
#(M2 ∪ M3 ∪ M5) = #(M2 ∪ M3 ∪ M5 \ M6 \ M10 \ M15 ∪ M30) = #(M2) + #(M3) + #(M5) – #(M6) – #(M10) – #(M15) + #(M30)
È necessario calcolare la cardinalità di tutti gli insiemi nella tabella…
| Insieme | Elementi | Cardinalità |
|---|---|---|
| I | 1, 2, 3, 4, …, 6000 | #(I) = 6000 |
| M2 | 2, 4, 6, 8, …, 6000 | #(M2) = 3000 |
| M3 | 3, 6, 9, 12, …, 6000 | #(M3) = 2000 |
| M5 | 5, 10, 15, 20, …, 6000 | #(M5) = 1200 |
| M6 = M2 ∩ M3 | 6, 12, 18, 24, …, 6000 | #(M6) = 1000 |
| M10 = M2 ∩ M5 | 10, 20, 30, 40, …, 6000 | #(M10) = 600 |
| M15 = M3 ∩ M5 | 15, 30, 45, 60, …, 6000 | #(M15) = 400 |
| M30 = M2 ∩ M3 ∩ M5 | 30, 60, 90, 120, …, 6000 | #(M30) = 200 |
| M2 ∪ M3 ∪ M5 | 2, 3, 4, 5, …, 6000 | #(M2 ∪ M3 ∪ M5) = ? |
| I \ (M2 ∪ M3 ∪ M5) | 1, 7, 11, 13, … | #(I \ (M2 ∪ M3 ∪ M5)) = ? |
Allora
#(M2 ∪ M3 ∪ M5) = 3000 + 2000 + 1200 – 1000 – 600 – 400 + 200 = 4400
e quindi
#(I \ (M2 ∪ M3 ∪ M5)) = 6000 – 4400 = 1600