Determinare il numero delle soluzioni dell’equazione ![]() .
.
Studia gli zeri della funzione ![]()
Esistenza
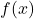 continua in R
continua in R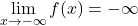

- Teorema degli zeri: esiste almeno uno zero in R
Unicità?
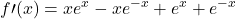
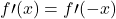
 per
per 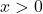
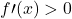 in R
in R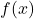 crescente in R
crescente in R- Un solo zero in R
Approssimazione
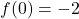
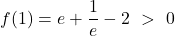
- Teorema degli zeri: esiste
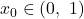 tale che
tale che 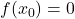 .
.