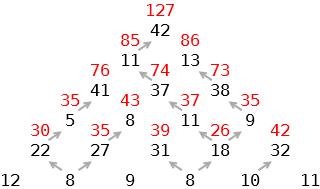
Data la seguente piramide di numeri, definiamo una discesa come “una sequenza di numeri ottenuti partendo dalla cima della piramide e passando per uno dei due numeri sottostanti, fino a giungere alla base della piramide”.
Inoltre, il valore di una discesa è la somma dei numeri della discesa.
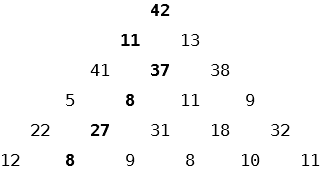
Nell’esempio, in corsivo grassetto è mostrata la discesa ottenuta partendo dalla cima e scendendo prima a sinistra, poi a destra e poi sempre a sinistra fino alla base.
I numeri di questa discesa sono (42,11,37,8,27,8) e la loro somma vale 133, che è il valore di questa discesa.
Se all’ultimo passo fossimo andati a destra la discesa sarebbe stata (42,11,37,8,27,9), con un valore pari a 134.
Nella piramide ci sono discese che valgono di più di 134.
Qual è il valore massimo MAX che si riesce a trovare in questa piramide?
E qual è il valore minimo MIN?
Soluzione: MAX=145, MIN=127.
Considera la scelta che faresti all’ultimo passo per ottenere il valore massimo.
Per esempio, in basso a sinistra sceglieresti 12 piuttosto che 8.
Il valore in blu, 34, è il valore massimo parziale corrispondente.

Se continui verso l’alto e ogni volta scegli il ramo con il valore in blu più alto arrivi in cima con il valore massimo raggiungibile.
Il valore massimo è 145 ottenuto con il percorso
(42, 13, 38, 9, 32, 11)
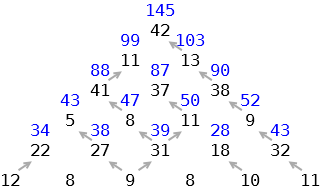
Analogamente per la ricerca del percorso con il valore minimo
(42, 11, 37, 11, 18, 8)