OII 2016-11-17 – Quesito 14

di

William abita molto vicino alla sua scuola.

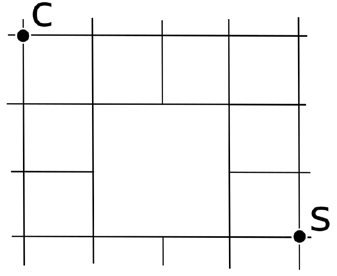
2016-14

Nella figura qui sopra, la casa di William è indicata con C e la sua scuola con S.
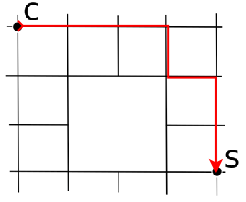
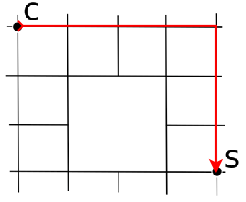
Il cammino minimo tra la casa e la scuola consiste in sette tratti, per esempio percorrendo il bordo esterno e poi scendendo fino alla scuola.

Ci sono tanti cammini minimi (sono quelli ottenibili andando, a ogni mossa, a destra oppure in basso).
Quanti sono?

19 | 17 | 15 | 18

Soluzione 1

Conta tutti i cammini disponibili da C a S

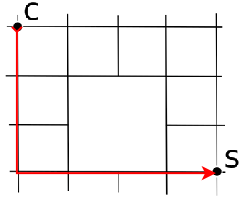
2016-14-1
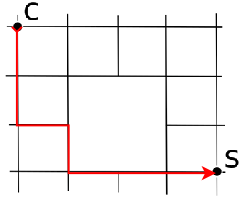
2016-14-2
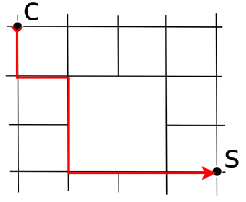
2016-14-3
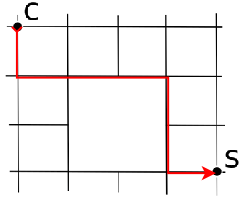
2016-14-4
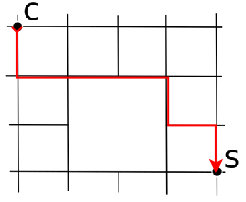
2016-14-5
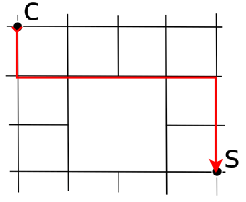
2016-14-6
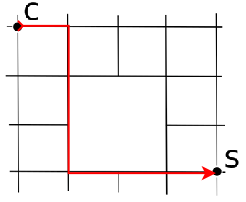
2016-14-7
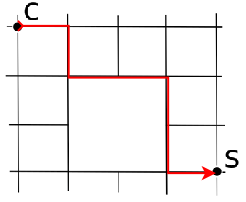
2016-14-8
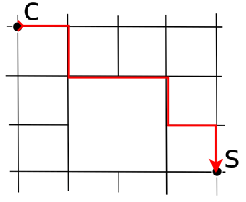
2016-14-9
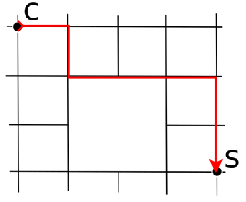
2016-14-10
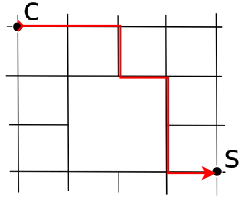
2016-14-11
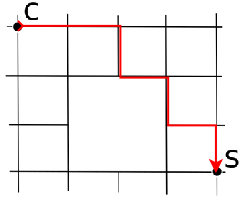
2016-14-12
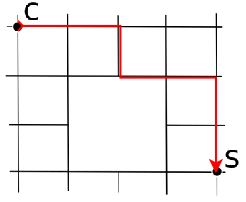
2016-14-13
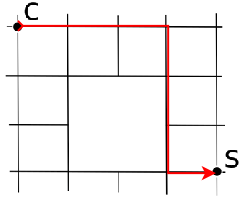
2016-14-14
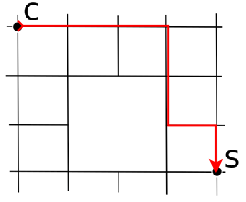
2016-14-15
2016-14-16
2016-14-17

Soluzione 2

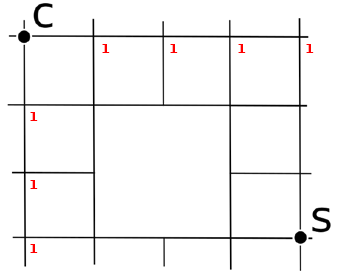
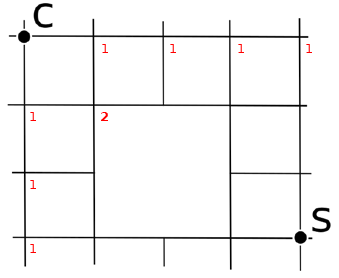
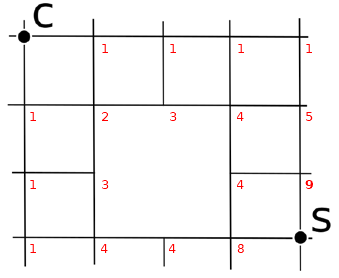
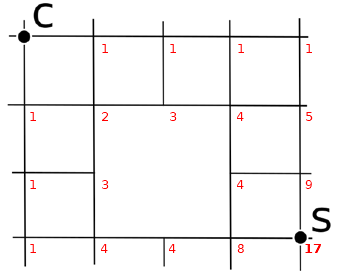
A partire da C, fino a raggiungere S, calcola il numero di cammini per raggiungere ciascun incrocio

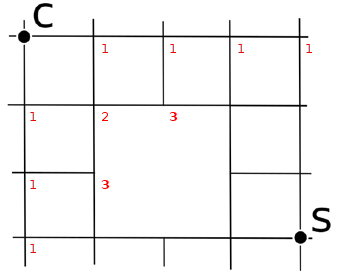
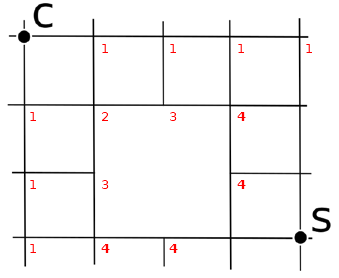
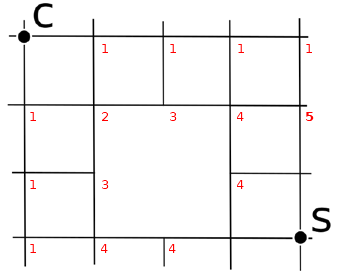
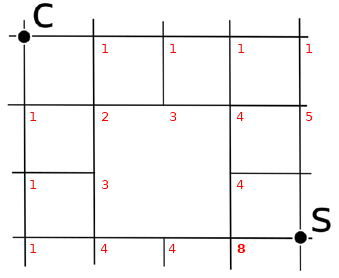
Soluzione 3

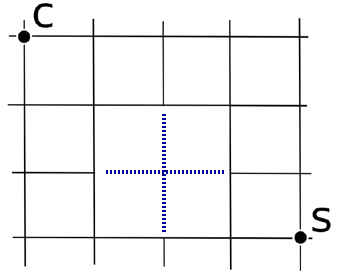
Considera la mappa comprensiva dell’incrocio mancante

Siano B=Basso e D=Destra le direzioni disponibili

Tutti i cammini da C a S  programmabili con 3 B e 4 D: \displaystyle \frac{7!}{4! \ 3!} = 35

I cammini da C all’incrocio mancante (con 2 B e 2 D): \displaystyle \frac{4!}{2! \ 2!} = 6

I cammini dall’incrocio mancante a S (con 1 B e 2 D): \displaystyle \frac{3!}{2! \ 1!} = 3

I cammini da C a S che passano per l’incrocio mancante: \displaystyle \frac{4!}{2! \ 2!} \cdot \frac{3!}{2! \ 1!} = 6 x 3 = 18

I cammini disponibili da C a S: \displaystyle \frac{7!}{4! \ 3!} – \displaystyle \frac{4!}{2! \ 2!} x \displaystyle \frac{3!}{2! \ 1!} = 35 – 6 x 3 = 17

Esercizio

Genera tutti i cammini!

  • Da C a S:
    BBBDDDD, BBDBDDD, BBDDBDD, BBDDDBD, BBDDDDB, BDBBDDD, BDBDBDD, BDBDDBD, BDBDDDB, BDDBBDD, BDDBDBD, BDDBDDB, BDDDBBD, BDDDBDB, BDDDDBB, DBBBDDD, DBBDBDD, DBBDDBD, DBBDDDB, DBDBBDD, DBDBDBD, DBDBDDB, DBDDBBD, DBDDBDB, DBDDDBB, DDBBBDD, DDBBDBD, DDBBDDB, DDBDBBD, DDBDBDB, DDBDDBB, DDDBBBD, DDDBBDB, DDDBDBB, DDDDBBB
  • Da C all’incrocio mancante:
    BBDD, BDDB, BDBD, DBBD, DBDB, DDBB
  • Dall’incrocio mancante a S:
    BDD, DBD, DDB
  • Da C a S che passano per l’incrocio mancante:
    BBDDBDD, BBDDDBD, BBDDDDB, BDBDBDD, BDBDDBD, BDBDDDB, BDDBBDD, BDDBDBD, BDDBDDB, DBBDBDD, DBBDDBD, DBBDDDB, DBDBBDD, DBDBDBD, DBDBDDB, DDBBBDD, DDBBDBD, DDBBDDB
  • Da C a S:
    BBBDDDD, BBDBDDD, BDBBDDD, BDDDBBD, BDDDBDB, BDDDDBB, DBBBDDD, DBDDBBD, DBDDBDB, DBDDDBB, DDBDBBD, DDBDBDB, DDBDDBB, DDDBBBD, DDDBBDB, DDDBDBB, DDDDBBB