QUESITI – Calcolo

di
ESAME
O.I.I.

Quesiti che richiedono la soluzione di equazioni, sistemi di equazioni, …

Anno 2007 PNI – Quesito 8

A Leonardo Eulero (1707-1783), di cui quest’anno ricorre centenario della nascita, si deve il seguente problema:
«Tre gentiluomini giocano insieme: nella prima partita il primo perde, a favore degli altri due, tanto denaro quanto ne possiede ciascuno di loro.
Nella successiva, il secondo gentiluomo perde a favore di ciascuno degli altri due tanto denaro quanto essi già ne possiedono.
Da ultimo, nella terza partita, il primo e il secondo guadagnano ciascuno dal terzo gentiluomo tanto denaro quanto ne avevano prima.
A questo punto smettono e trovano che ciascuno ha la stessa somma, cioè 24 luigi.
Si domanda con quanto denaro si sedette a giocare».

OII Allenamenti 2004 – 3

Vogliamo calcolare in quanti modi diversi possiamo ottenere il numero 120 come somma di due numeri interi e positivi.

OII 18-11-2005 – 3

Quanti modelli di macchine di Formula 1 ha Mario se sono tutte Ferrari meno tre, sono tutte McLaren meno due ed ha anche una Williams?

Risposte:

  1. 3
  2. 4
  3. 5
  4. 6.

SOLUZIONE

Siano

  • F = numeri di Ferrari
  • M = … McLaren
  • W = … Williams
  • N = … macchinine.

I fatti noti, in ordine

\displaystyle \begin{cases} F = N-3 \\ M = N-2 \\ W = 1 \\ F+M+W=N \end{cases}

…

\displaystyle \begin{cases} F=1 \\ M=2 \\ W=1 \\ N=4\end{cases}

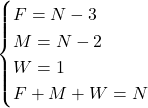
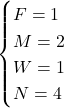
OII 18-11-2005 – 7

A Policrate che gli domandava quanti erano i suoi allievi, così rispose Pitagora:

  • I miei allievi possono essere suddivisi in insiemi disgiunti.
  • In particolare
    • la metà coltiva la matematica
    • la quarta parte si dedica allo studio della natura
    • la settima parte ascolta con religioso silenzio le mie parole
    • inoltre ci sono tre allievi che non fanno nessuna delle cose precedenti.

Quanti erano gli allievi di Pitagora?

SOLUZIONE

\displaystyle \frac{N}{2}+\frac{N}{4}+\frac{N}{7}+3 = N

…

N=28

OII 23-11-2007 – Quesito 9

La regione organizza un torneo di calcio fra le classi di scuola superiore.
Al torneo partecipano 380 squadre.
Il torneo è a eliminazione diretta e quindi ogni sfida ha un vincitore.
Ad ogni turno le squadre vengono divise in coppie: le due squadre si sfidano e la vincente passa al turno successivo.
Se ad un turno il numero delle squadre rimaste è dispari si sorteggia una squadra che passa automaticamente il turno.
Qual è il numero totale di partite giocate fra tutte le squadre per determinare la squadra vincente?

OII 3-12-2009 – Quesito 6

Un regista vuole sapere quante proiezioni del suo film sono state fatte in un certo cinema.
L’usciere del cinema in cui il film è stato proiettato gli fornisce queste informazioni:

  1. Alla prima proiezione c’era un solo spettatore.
  2. A ogni nuova proiezione il numero degli spettatori è cresciuto di un’unità rispetto alla proiezione precedente.
  3. Il numero totale di spettatori durante tutte le proiezioni è stato 820.

Quante proiezioni ci sono state?

OII 23-2-2021 – 5

Ad una festa sono stati invitati diversi amici, si sa che a 10 di questi piacciono i treni, a 10 piacciono le macchine da corsa e a 10 gli aerei.
Ogni amico può avere anche più di una passione!

Si sa inoltre:

  • solo uno ha la passione per tutti 3 i mezzi
  • a 7 amici piacciano i treni ma non gli aerei
  • a 5 amici piacciono solo le macchine
  • a 8 amici piacciano gli aerei ma non le macchine

Quanti sono gli amici in tutto?

SOLUZIONE

Dividi gli amici in categorie distinte rispetto alle loro passioni

  • A = Solo aerei
  • M = Solo macchine
  • T = Solo treni
  • AM = Aerei e macchine
  • AT = Aerei e treni
  • MT = Macchine e treni
  • AMT = Aerei, macchine e treni

I fatti noti, in ordine

\displaystyle \begin{cases} T+AT+MT+AMT = 10 \\ M+AM+MT+AMT = 10 \\ A+AM+AT+AMT = 10 \\ AMT = 1 \\ T+MT = 7 \\ M = 5 \\ A+AT = 8\end{cases}

…

\displaystyle \begin{cases} A=6 \\ M=5 \\ T=4 \\ AM=1 \\ AT=2 \\ AT=2 \\ MT = 3 \\ AMT=1 \end{cases}

A+M+T+AM+AT+MT+AMT
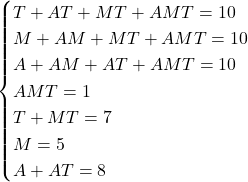
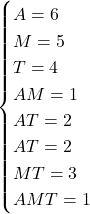
= 6+5+4+1+2+3+1
= 22

OII 20-11-2019 – 1

Valerio e Martina hanno scoperto di aver ereditato una piccola somma da un lontano parente venuto a mancare da poco.
Il testamento contiene le indicazioni sull’importo che spetta a ciascuno dei due ragazzi, ovvero quanto segue:

“Vorrei che il doppio di quanto spetti a Martina sia pari al triplo di quanto spetti a Valerio; vorrei inoltre che il doppio di quanto spetti a Valerio, sommato con il triplo di quanto spetti a Martina, sia pari a 13.000 euro.”

Qual è il valore complessivo VALTOT dell’eredità di Martina e Valerio?

SOLUZIONE

\displaystyle \begin{cases} 2M=3V \\ 2V+3M = 13000\end{cases}

…

\displaystyle \begin{cases} M=3000 \\ V = 2000\end{cases}

\displaystyle M+V
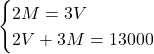
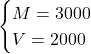
= 3000+2000
= 5000