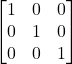Con l’eliminazione di Gauss-Jordan si può calcolare la matrice inversa.
Considera la matrice che si ottiene affiancando alle colonne di A le colonne della matrice Identità (dello stesso ordine)
![]()

Applica l’eliminazione di Gauss-Jordan alla prima metà.
Le stesse operazioni agiscono anche sulla seconda metà
![]()
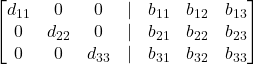
Ottieni una matrice diagonale, adesso dividi gli elementi di ogni riga per l’elemento della diagonale principale.
Le stesse operazioni agiscono anche sulla seconda metà
![]()
![]()
![]()
Ottieni la matrice identità affiancata dalla matrice G.
La matrice G ha trasformato la matrice A nella matrice identità, quindi è la sua inversa!
![]()
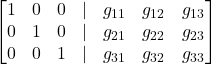
Esempio 2×2
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
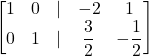
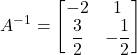
Controlla…
![]()
= 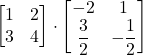
= 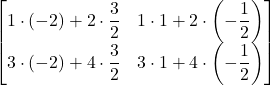
= ![]()
= ![]()
Controlla…
![]()
= 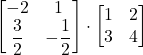
= 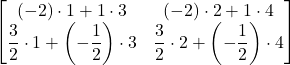
= 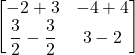
= ![]()
Esempio 3×3
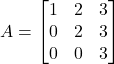

![]()
![]()

![]()
![]()

![]()
![]()
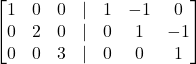
![]()
![]()
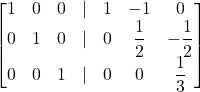
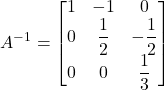
Controlla…
![]()
= 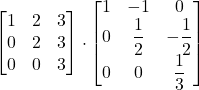
= 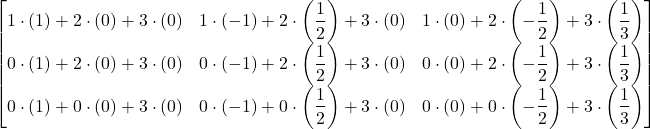
= 
= 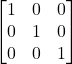
Controlla…
![]() =
= 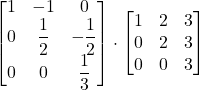 = … =
= … =