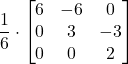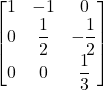Considera una matrice A

Calcola tutti i determinanti delle sottomatrici di A.
I minori complementari…

Calcola tutti i cofattori ![]() .
.
Aggiungi il segno ai minori complementari, ![]()
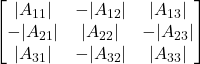
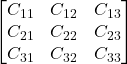
Considera la trasposta dei cofattori
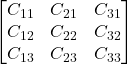
Dividi tutto per il determinante di A.
Moltiplica per uno scalare.

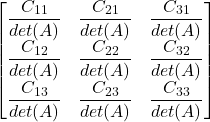
Riassunto: ogni elemento della trasposta di A è dato dal simmetrico del cofattore diviso il determinante di A…
![]()
Esempio 2×2
![]()
Il determinante di A: ![]()
Calcola i determinanti di tutte le sottomatrici
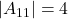 ,
, 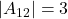
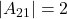 ,
, 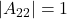
![]()
Aggiungi i segni
![]()
Calcola la trasposta
![]()
Dividi per il determinante di A
![]()
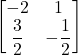
Esempio 3×3

Il determinante di A: ![]()
Calcola tutti i determinanti delle sottomatrici
![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]()

Aggiungi i segni
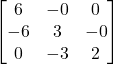
Calcola la trasposta
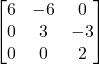
Dividi per il determinante di A