Isaac Newton, Philosophiae Naturalis Principia Mathematica, 1687
La funzione polinomiale di grado n passante per n+1 punti.
Le ascisse dei punti devono essere tutte diverse.
Grado = 1
![]()
Grado = 2
![]()
Grado = 3
![]()
Grado = n
![]()
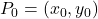
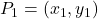
- …
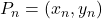
Grado = 1
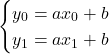
…
…
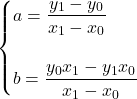
Versione 1
![]()
Versione 2
![]()
oppure
![]()
Versione 3
![]()
oppure
![]()
oppure
![]()
Grado = 2
Ripetendo tutti i passaggi si ripropone il problema di avere una formulazione di semplice memorizzazione…
![]()
![]()
Osserva
![]()
![]() =
= ![]()
![]() =
= ![]() =
= 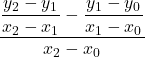
Dimostrazione
Deve essere ![]() , quindi…
, quindi…
![]()
![]()
![]()
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
![]()
![]()
![]() =
= 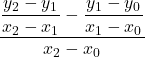 =
= ![]() =
= ![]()
Grado = n
Lo schema generale è il polinomio di Newton
![]()
![]() +
+ ![]() +
+ ![]()
![]()
Con
![]()
![]() =
= ![]()
![]() =
= ![]()
…
![]() =
= ![]()