Verificare che l’equazione ![]() ammette tre radici reali.
ammette tre radici reali.
Di una di esse, quella compresa tra 0 e 1, se ne calcoli un’approssimazione applicando uno dei metodi numerici studiati.
Sia
f(x) = ![]()
Osserva
- f(x) continua…
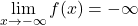
 , almeno uno zero
, almeno uno zero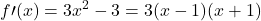
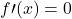 per
per 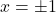 , due punti notevoli
, due punti notevoli- f(-1) = +3
- f(+1) = -1, punti notevoli discordi
- f(-2) = -1
- f(-1) = +3, segni discordi in [-2, -1], almeno uno zero in (-2, -1)
- f(+1) = -1, segni discordi in [-1, +1], almeno uno zero in (-1, +1)
- f(+2) = +3, segni discordi in [+1, +2], almeno uno zero in (+1, +2)
Se ne calcoli…