Wikipedia: Algoritmo di Euclide
L’algoritmo di Euclide permette di calcolare il massimo comun divisore, MCD, tra due numeri interi (senza passare per la fattorizzazione).

Algoritmo

Dati due numeri naturali a e b

se b è zero allora la risposta è a
altrimenti si divide a per b e si assegna ad r il resto della divisione
- se r=0 allora la risposta è b
- altrimenti a ⇐ b e b ⇐ r e si ripete nuovamente la divisione.

MCD(70, 15)

  a |  b | quoziente | resto
----+----+-----------+-------
 70 | 15 | 70:15 = 4 | 10
 15 | 10 | 15:10 = 1 |  5
 10 |  5 | 10: 5 = 2 |  0

MCD(70, 15) = 5

MCD(15, 70)

Se a < b si scambiano di posto dopo il primo passo

  a |  b | quoziente | resto
----+----+-----------+-------
 15 | 70 | 15:70 = 0 | 15  
 70 | 15 | 70:15 = 4 | 10 
 15 | 10 | 15:10 = 1 |  5 
 10 |  5 | 10: 5 = 2 |  0

MCD(15, 70) = 5

MCD(71, 15)

  a |  b | quoziente | resto
----+----+-----------+-------
 71 | 15 | 71:15 = 4 | 11  
 15 | 11 | 15:11 = 1 |  4 
 11 |  4 | 11: 4 = 2 |  3 
  4 |  3 |  4: 3 = 1 |  1 
  3 |  1 |  3: 1 = 3 |  0

MCD(71, 15)=1.

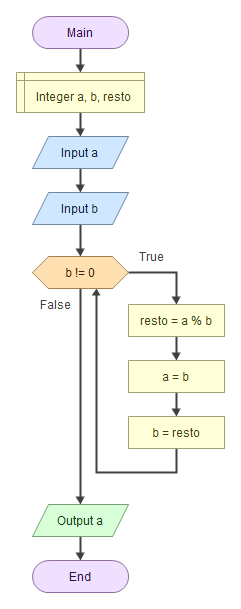
L’algoritmo precedente può essere trasformato in un programma di alto livello dopo qualche modifica per adattarlo alla esigenze della programmazione strutturata.

Dati due numeri naturali a e b

mentre b è diverso da 0 ripeti

r ⇐ resto della divisione intera tra a e b
a ⇐ b
b ⇐ r

la risposta è a

  a |  b |           |  r 
----+----+-----------+----
 70 | 15 | 70:15 = 4 | 10  
 15 | 10 | 15:10 = 1 |  5 
 10 |  5 | 10: 5 = 2 |  0 
  5 |  0 |           |

Versione ricorsiva

$\displaystyle MCD(a, b)=\left\{ \begin{array}{ll}a&b=0\\ MCD(b, a\ mod\ b) & \text{altrimenti}\end{array} \right$

Esempio

MCD(70, 15) = MCD(15, 70 Mod 15)
            = MCD(15, 10) = MCD(10, 15 Mod 10)
                          = MCD(10, 5) = MCD(5, 10 Mod 5)
                                       = MCD(5, 0)
                                       = 5
                          = 5
            = 5
= 5