Dati n oggetti tutti diversi (a, b, c, …) la scrittura Cn,k significa
- In quanti modi si possono scegliere k oggetti, considerando uguali due sequenze con gli stessi oggetti
- Quante squadre di k elementi si possono comporre avendo a disposizione n persone
- Quante combinazioni semplici di n elementi di classe k
Prova…
| n | k = 0 | k = 1 | k = 2 | k = 3 | k = 4 | k = 5 |
|---|---|---|---|---|---|---|
| 0 | {} | |||||
| 1 | {} | A | ||||
| 2 | {} | A | AB | |||
| 3 | {} | A | AB AC | ABC | ||
| 4 | {} | A | AB AC AD | ABC ABD ACD | ABCD | |
| 5 | {} | A | AB AC AD AE BC BD BE CD CE DE | ABC ABD ABE ACD ACE ADE | ABCD ABCE ABDE ACDE | ABCDE |
| 6 | {} | A | AB AC AD AE AF | ABC ABD ABE ABF ACD ACE ACF ADE ADF | ABCD ... CDEF | ABCDE ... BCDEF |
| 7 | {} | A | AB AC AD AE AF AG | ABC ... EFG | ABCD ... DEFG | ABCDE ... CDEFG |
| 8 | {} | ... | AB ... GH | ABC ... FGH | ABCD ... EFGH | ABCDE ... DEFGH |
Ecco i conti della tabella precedente
+---+----------------------------+
| | 0 1 2 3 4 5 6 7 8 |
+---+----------------------------+
| 0 | 1 |
| 1 | 1 1 |
| 2 | 1 2 1 |
| 3 | 1 3 3 1 |
| 4 | 1 4 6 4 1 |
| 5 | 1 5 10 10 5 1 |
| 6 | 1 6 15 20 15 6 1 |
| 7 | 1 7 21 35 35 21 7 1 |
| 8 | 1 8 28 56 70 56 28 8 1 |
+---+----------------------------+
Osserva
- Scelgo il 1° simbolo tra n
- Scelgo il 2° simbolo tra n-1 rimanenti
- …
- Scelgo il k° simbolo tra n-k+1 rimanenti
Si ottengono ![]() sequenze ma non sono tutte diverse…
sequenze ma non sono tutte diverse…
Ci sono ![]() sequenze per ogni scelta di k simboli diversi, quindi i valori di
sequenze per ogni scelta di k simboli diversi, quindi i valori di ![]() , coefficiente binomiale n sopra k, sono
, coefficiente binomiale n sopra k, sono
![]() =
= ![]() =
= ![]() =
= ![]()
Proprietà 1
Dall’osservazione della tabella risulta
![]()
+---+----------------------------+
| | 0 1 2 3 4 5 6 7 8 |
+---+----------------------------+
| 0 | 1 |
| 1 | 1 1 |
| 2 | 1 2 1 |
| 3 | 1 3 3 1 |
| 4 | 1 4 6 4 1 |
| 5 | 1 5 10 10 5 1 |
| 6 | 1 6 15 20 15 6 1 |
| 7 | 1 7 21 35 35 21 7 1 |
| 8 | 1 8 28 56 70 56 28 8 1 |
+---+----------------------------+
![]()
+---+----------------------------+
| | 0 1 2 3 4 5 6 7 8 |
+---+----------------------------+
| 0 | 1 |
| 1 | 1 1 |
| 2 | 1 2 1 |
| 3 | 1 3 3 1 |
| 4 | 1 4 6 4 1 |
| 5 | 1 5 10 10 5 1 |
| 6 | 1 6 15 20 15 6 1 |
| 7 | 1 7 21 35 35 21 7 1 |
| 8 | 1 8 28 56 70 56 28 8 1 |
+---+----------------------------+
In generale
![]()
Proprietà 2
![]()
+---+----------------------------+
| | 0 1 2 3 4 5 6 7 8 |
+---+----------------------------+
| 0 | 1 |
| 1 | 1 1 |
| 2 | 1 2 1 |
| 3 | 1 3 3 1 |
| 4 | 1 4 6 4 1 |
| 5 | 1 5 10 10 5 1 |
| 6 | 1 6 15 20 15 6 1 |
| 7 | 1 7 21 35 35 21 7 1 |
| 8 | 1 8 28 56 70 56 28 8 1 |
+---+----------------------------+
Osserva
- 2 = 1+1
- 10 = 6+4 = 4+6
- 8 = 7+1 = 1+7
- 70 = 35+35
- …
Proprietà 3
![]()
Esempi
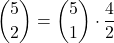 =
= 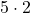 = 10
= 10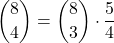 =
= 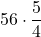 = 70
= 70- …
Triangolo di Tartaglia
Le proprietà 1 e 2 della tabella sono più evidenti se si cambia la disposizione dei valori
+---+---------------------------------------------------+
| 0 | 1 |
| 1 | 1 1 |
| 2 | 1 2 1 |
| 3 | 1 3 3 1 |
| 4 | 1 4 6 4 1 |
| 5 | 1 5 10 10 5 1 |
| 6 | 1 6 15 20 15 6 1 |
| 7 | 1 7 21 35 35 21 7 1 |
| 8 | 1 8 28 56 70 56 28 8 1 |
+---+---------------------------------------------------+