Con uno dei metodi di quadratura studiati, si calcoli un’approssimazione dell’integrale definito ![]() e …
e …
Metodo dei rettangoli con altezze nel punto centrale
Un rettangolo
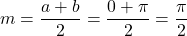
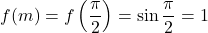
- Area =
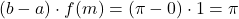
Al variare di n
Le ascisse per i punti centrali di ogni intervallo
- x = a+h/2, a+h/2+h, a+h/2+2h, …, a+h/2+(n-1)h
| n | h | i* | xi* | yi* | Area | = |
| 1 | 0* | = | ||||
| h/2 | = | |||||
| = 3,141593 | ||||||
| n | h | i* | xi* | yi* | Area | = |
| 2 | 0* | = 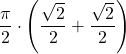 | ||||
| h/2 | 1* | = | ||||
| = 2,221442 | ||||||
| n | h | i* | xi* | yi* | Area | = |
| 3 | 0* | = | ||||
| h/2 | 1* | = | ||||
| 2* | = 2,094395 |