Con uno dei metodi di quadratura studiati, si calcoli un’approssimazione dell’integrale definito ![]() e …
e …
Metodo dei rettangoli con altezze di destra
| n | h | i | xi | yi | Area | = |
| 1 | 1 | = | ||||
| = 0,0 | ||||||
| n | h | i | xi | yi | Area | = |
| 2 | 1 | = | ||||
| 2 | = | |||||
| = 1,570796 | ||||||
| n | h | i | xi | yi | Area | = |
| 3 | 1 | = 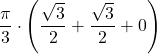 | ||||
| 2 | = | |||||
| 3 | = 1,813799 | |||||
| n | h | i | xi | yi | Area | = |
| 4 | 1 | = 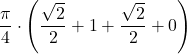 | ||||
| 2 | = 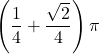 | |||||
| 3 | = 1,896119 | |||||
| 4 | ||||||
| n | h | i | xi | yi | Area | = |
| 6 | 1 | = 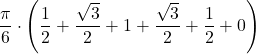 | ||||
| 2 | = 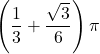 | |||||
| 3 | = 1,954097 | |||||
| 4 | ||||||
| 5 | ||||||
| 6 |